Интересный проект представил Paul Bishop — Arduino как анализатор звукового спектра с выводом спектрограммы на телевизор. На самом деле не телевизор, а экран DVD-плеера, но способ вывода абсолютно тот же. Для вывода была использована Arduino библиотека TVout, которая позволяет выводить сигнал на телевизор через RCA коннектор в формате PAL или NTSC. Картинка черно-белая и идет с разрешением 128х96. При таком разрешение на экран можно вывести 12 строк по 16 символов при размере шрифта 8х8.
Paul использовал контроллер Adafruit Boarduino, но подойдет любой 5 вольтовый, кроме самых старых моделей Arduino на Atmel ATmega168, так как у них просто недостаточно памяти.
Звук снимается с микрофона и усиливается через 2n3904 NPN транзистор так, как показано на схеме и считывается контроллером на аналоговом входе 0. Для частотного разложения звука используются быстрое преобразование Фурье. Автору не пришлось писать эту часть кода, он использовал готовую библиотеку FFT, код которой мы приводим ниже. Эта библиотека целиком написана на С и отлично работает на Atmega 328 и имеющихся в распоряжении 2кБ памяти. Для того, чтобы использовать эту библиотеку код надо поместить в файлы .cpp и .h в директории \libraries\FFT.
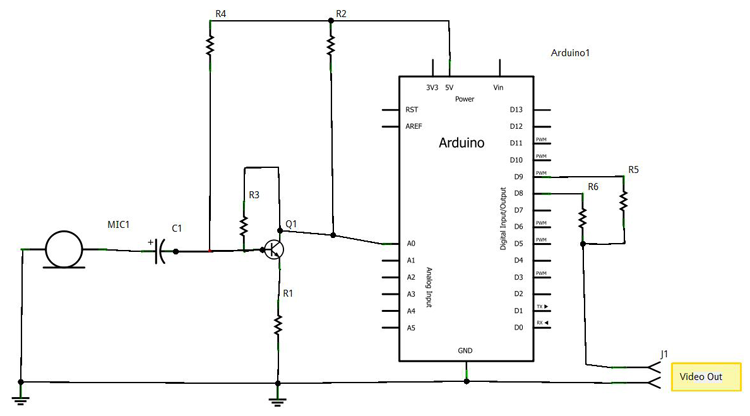
Компоненты:
(1шт.) 2n3904 NPN Транзистор [Q1]
(3шт.) 1k Ohm Резистор [R2,R4,R5]
(1шт.) 330 Ohm Резистор [R6]
(1шт.) 10k Ohm Резистор [R1]
(1шт.) 100k Ohm Резистор [R3]
(1шт.) Конденсатор электролит., 3.3MF [C1]
(1шт.) Микрофон [MIC1]
Код библиотеки FFT (быстрое преобразование Фурье):
файл fix_fft.h:
#ifndef FIXFFT_H |
#define FIXFFT_H |
#include <WProgram.h> |
/* |
fix_fft() - perform forward/inverse fast Fourier transform. |
fr[n],fi[n] are real and imaginary arrays, both INPUT AND |
RESULT (in-place FFT), with 0 <= n < 2**m; set inverse to |
0 for forward transform (FFT), or 1 for iFFT. |
*/ |
int fix_fft(char fr[], char fi[], int m, int inverse); |
/* |
fix_fftr() - forward/inverse FFT on array of real numbers. |
Real FFT/iFFT using half-size complex FFT by distributing |
even/odd samples into real/imaginary arrays respectively. |
In order to save data space (i.e. to avoid two arrays, one |
for real, one for imaginary samples), we proceed in the |
following two steps: a) samples are rearranged in the real |
array so that all even samples are in places 0-(N/2-1) and |
all imaginary samples in places (N/2)-(N-1), and b) fix_fft |
is called with fr and fi pointing to index 0 and index N/2 |
respectively in the original array. The above guarantees |
that fix_fft "sees" consecutive real samples as alternating |
real and imaginary samples in the complex array. |
*/ |
int fix_fftr(char f[], int m, int inverse); |
#endif |
fix_fft.cpp:
#include <avr/pgmspace.h> |
#include "fix_fft.h" |
#include <WProgram.h> |
/* fix_fft.c - Fixed-point in-place Fast Fourier Transform */ |
/* |
All data are fixed-point short integers, in which -32768 |
to +32768 represent -1.0 to +1.0 respectively. Integer |
arithmetic is used for speed, instead of the more natural |
floating-point. |
For the forward FFT (time -> freq), fixed scaling is |
performed to prevent arithmetic overflow, and to map a 0dB |
sine/cosine wave (i.e. amplitude = 32767) to two -6dB freq |
coefficients. The return value is always 0. |
For the inverse FFT (freq -> time), fixed scaling cannot be |
done, as two 0dB coefficients would sum to a peak amplitude |
of 64K, overflowing the 32k range of the fixed-point integers. |
Thus, the fix_fft() routine performs variable scaling, and |
returns a value which is the number of bits LEFT by which |
the output must be shifted to get the actual amplitude |
(i.e. if fix_fft() returns 3, each value of fr[] and fi[] |
must be multiplied by 8 (2**3) for proper scaling. |
Clearly, this cannot be done within fixed-point short |
integers. In practice, if the result is to be used as a |
filter, the scale_shift can usually be ignored, as the |
result will be approximately correctly normalized as is. |
Written by: Tom Roberts 11/8/89 |
Made portable: Malcolm Slaney 12/15/94 <a href="mailto:malcolm@interval.com">malcolm@interval.com</a> |
Enhanced: Dimitrios P. Bouras 14 Jun 2006 <a href="mailto:dbouras@ieee.org">dbouras@ieee.org</a> |
Modified for 8bit values David Keller 10.10.2010 |
*/ |
#define N_WAVE 256 /* full length of Sinewave[] */ |
#define LOG2_N_WAVE 8 /* log2(N_WAVE) */ |
/* |
Since we only use 3/4 of N_WAVE, we define only |
this many samples, in order to conserve data space. |
*/ |
const prog_int8_t Sinewave[N_WAVE-N_WAVE/4] PROGMEM = { |
0, 3, 6, 9, 12, 15, 18, 21, |
24, 28, 31, 34, 37, 40, 43, 46, |
48, 51, 54, 57, 60, 63, 65, 68, |
71, 73, 76, 78, 81, 83, 85, 88, |
90, 92, 94, 96, 98, 100, 102, 104, |
106, 108, 109, 111, 112, 114, 115, 117, |
118, 119, 120, 121, 122, 123, 124, 124, |
125, 126, 126, 127, 127, 127, 127, 127, |
127, 127, 127, 127, 127, 127, 126, 126, |
125, 124, 124, 123, 122, 121, 120, 119, |
118, 117, 115, 114, 112, 111, 109, 108, |
106, 104, 102, 100, 98, 96, 94, 92, |
90, 88, 85, 83, 81, 78, 76, 73, |
71, 68, 65, 63, 60, 57, 54, 51, |
48, 46, 43, 40, 37, 34, 31, 28, |
24, 21, 18, 15, 12, 9, 6, 3, |
0, -3, -6, -9, -12, -15, -18, -21, |
-24, -28, -31, -34, -37, -40, -43, -46, |
-48, -51, -54, -57, -60, -63, -65, -68, |
-71, -73, -76, -78, -81, -83, -85, -88, |
-90, -92, -94, -96, -98, -100, -102, -104, |
-106, -108, -109, -111, -112, -114, -115, -117, |
-118, -119, -120, -121, -122, -123, -124, -124, |
-125, -126, -126, -127, -127, -127, -127, -127, |
/*-127, -127, -127, -127, -127, -127, -126, -126, |
-125, -124, -124, -123, -122, -121, -120, -119, |
-118, -117, -115, -114, -112, -111, -109, -108, |
-106, -104, -102, -100, -98, -96, -94, -92, |
-90, -88, -85, -83, -81, -78, -76, -73, |
-71, -68, -65, -63, -60, -57, -54, -51, |
-48, -46, -43, -40, -37, -34, -31, -28, |
-24, -21, -18, -15, -12, -9, -6, -3, */ |
}; |
/* |
FIX_MPY() - fixed-point multiplication & scaling. |
Substitute inline assembly for hardware-specific |
optimization suited to a particluar DSP processor. |
Scaling ensures that result remains 16-bit. |
*/ |
inline char FIX_MPY(char a, char b) |
{ |
|
//Serial.println(a); |
//Serial.println(b); |
|
|
/* shift right one less bit (i.e. 15-1) */ |
int c = ((int)a * (int)b) >> 6; |
/* last bit shifted out = rounding-bit */ |
b = c & 0x01; |
/* last shift + rounding bit */ |
a = (c >> 1) + b; |
/* |
Serial.println(Sinewave[3]); |
Serial.println(c); |
Serial.println(a); |
while(1);*/ |
return a; |
} |
/* |
fix_fft() - perform forward/inverse fast Fourier transform. |
fr[n],fi[n] are real and imaginary arrays, both INPUT AND |
RESULT (in-place FFT), with 0 <= n < 2**m; set inverse to |
0 for forward transform (FFT), or 1 for iFFT. |
*/ |
int fix_fft(char fr[], char fi[], int m, int inverse) |
{ |
int mr, nn, i, j, l, k, istep, n, scale, shift; |
char qr, qi, tr, ti, wr, wi; |
n = 1 << m; |
/* max FFT size = N_WAVE */ |
if (n > N_WAVE) |
return -1; |
mr = 0; |
nn = n - 1; |
scale = 0; |
/* decimation in time - re-order data */ |
for (m=1; m<=nn; ++m) { |
l = n; |
do { |
l >>= 1; |
} while (mr+l > nn); |
mr = (mr & (l-1)) + l; |
if (mr <= m) |
continue; |
tr = fr[m]; |
fr[m] = fr[mr]; |
fr[mr] = tr; |
ti = fi[m]; |
fi[m] = fi[mr]; |
fi[mr] = ti; |
} |
l = 1; |
k = LOG2_N_WAVE-1; |
while (l < n) { |
if (inverse) { |
/* variable scaling, depending upon data */ |
shift = 0; |
for (i=0; i<n; ++i) { |
j = fr[i]; |
if (j < 0) |
j = -j; |
m = fi[i]; |
if (m < 0) |
m = -m; |
if (j > 16383 || m > 16383) { |
shift = 1; |
break; |
} |
} |
if (shift) |
++scale; |
} else { |
/* |
fixed scaling, for proper normalization -- |
there will be log2(n) passes, so this results |
in an overall factor of 1/n, distributed to |
maximize arithmetic accuracy. |
*/ |
shift = 1; |
} |
/* |
it may not be obvious, but the shift will be |
performed on each data point exactly once, |
during this pass. |
*/ |
istep = l << 1; |
for (m=0; m<l; ++m) { |
j = m << k; |
/* 0 <= j < N_WAVE/2 */ |
wr = pgm_read_word_near(Sinewave + j+N_WAVE/4); |
/*Serial.println("asdfasdf"); |
Serial.println(wr); |
Serial.println(j+N_WAVE/4); |
Serial.println(Sinewave[256]); |
Serial.println("");*/ |
wi = -pgm_read_word_near(Sinewave + j); |
if (inverse) |
wi = -wi; |
if (shift) { |
wr >>= 1; |
wi >>= 1; |
} |
for (i=m; i<n; i+=istep) { |
j = i + l; |
tr = FIX_MPY(wr,fr[j]) - FIX_MPY(wi,fi[j]); |
ti = FIX_MPY(wr,fi[j]) + FIX_MPY(wi,fr[j]); |
qr = fr[i]; |
qi = fi[i]; |
if (shift) { |
qr >>= 1; |
qi >>= 1; |
} |
fr[j] = qr - tr; |
fi[j] = qi - ti; |
fr[i] = qr + tr; |
fi[i] = qi + ti; |
} |
} |
--k; |
l = istep; |
} |
return scale; |
} |
/* |
fix_fftr() - forward/inverse FFT on array of real numbers. |
Real FFT/iFFT using half-size complex FFT by distributing |
even/odd samples into real/imaginary arrays respectively. |
In order to save data space (i.e. to avoid two arrays, one |
for real, one for imaginary samples), we proceed in the |
following two steps: a) samples are rearranged in the real |
array so that all even samples are in places 0-(N/2-1) and |
all imaginary samples in places (N/2)-(N-1), and b) fix_fft |
is called with fr and fi pointing to index 0 and index N/2 |
respectively in the original array. The above guarantees |
that fix_fft "sees" consecutive real samples as alternating |
real and imaginary samples in the complex array. |
*/ |
int fix_fftr(char f[], int m, int inverse) |
{ |
int i, N = 1<<(m-1), scale = 0; |
char tt, *fr=f, *fi=&f[N]; |
if (inverse) |
scale = fix_fft(fi, fr, m-1, inverse); |
for (i=1; i<N; i+=2) { |
tt = f[N+i-1]; |
f[N+i-1] = f[i]; |
f[i] = tt; |
} |
if (! inverse) |
scale = fix_fft(fi, fr, m-1, inverse); |
return scale; |
} |
Arduino скетч:
#include <TVout.h> |
#include <fix_fft.h> |
TVout TV; |
char im[128], data[128], lastpass[64]; |
char x=32, ylim=90; |
int i=0,val; |
void setup() |
{
|
TV.begin(_NTSC,128,96);
// Initialize TV output, 128x96. |
TV.print_str(2,2," Realtime Arduino"); // TVout lib uses x,y for print |
TV.print_str(2,11," Spectrum Analyzer"); // statements. 8x8 default font. |
analogReference(DEFAULT);
// Use default (5v) aref voltage. |
for (int z=0; z<64; z++) {lastpass[z]=80;}; // fill the lastpass[] array with dummy data |
}; |
void loop() |
{ |
for (i=0;
i < 128;
i++){
// We don't go for clean timing here, it's |
val
=
analogRead(0);
// better to get somewhat dirty data fast |
data[i]
= val/4
-128;
// than to get data that's lab-accurate |
im[i]
=
0;
// but too slow, for this application. |
}; |
fix_fft(data,im,7,0); |
|
for (i=1;
i<
64;i++){
// In the current design, 60Hz and noise |
data[i] = sqrt(data[i] * data[i] + im[i] * im[i]); // in general are a problem. Future designs |
TV.draw_line(i+x,lastpass[i],i+x,ylim,0); // and code may fix this, but for now, I |
TV.draw_line(i+x,ylim,i+x,ylim-data[i],1); // skip displaying the 0-500hz band completely. |
lastpass[i]=ylim-data[i];
// if you insist, initialize the loop with 0 |
};
// rather than 1. |
}; |
Оригинальная статья на блоге автора.