Согласование импедансов антенны и кабеля.
1. Согласование сопротивлений, не содержащих реактивную составляющую.
Эта статья посвящена тому, как рассчитать элементы согласования нагрузки(антенны) с кабелем.
Существует множество программ для этой цели, но как быть если ваш компьютер сломался, или программа запорчена, а вам надо рассчитать согласование? Вот для этого случая и надо знать методику расчета. Методика не сложная, поэтому освоить ее - под силу каждому. Расчет элементов согласования - это конечная цель измерений импеданса антенны, нагрузки кабеля.
Ранее уже рассматривался вопрос важности согласования импеданса нагрузки и волнового сопротивления коаксиального кабеля, при помощи которого производится питание антенны. Я не буду описывать теорему, доказывающую, что максимальный сигнал с генератора, у которого внутреннее сопротивление равно R, можно получить только в том случае, если сопротивление нагрузки этого генератора, будет точно равно сопротивлению генератора R.
В нашем случае, кабель(источник)с известным волновым сопротивлением, будем замещать источником сигнала, последовательно с которым включено сопротивление, равное волновому сопротивлению кабеля. Нагрузку(импеданс антенны), будем изображать резистором с последовательно включенным конденсатором, или индуктивностью. Задача будет состоять в том, как согласовать между собой эти два, в большинстве случаев, различных сопротивления.
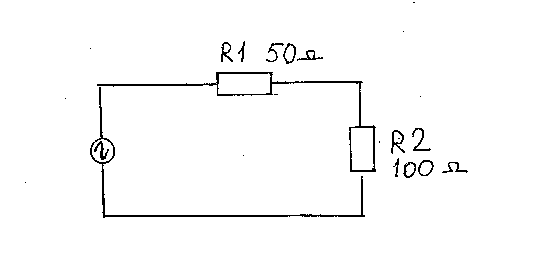
В качестве примера, на Рис.1 приведена эквивалентная схема, на которой изображен кабель 50 Ом, питающий антенну, которая имеет импеданс 100 Ом.

Рис.1
Мы видим, что нагрузка в 100 Ом, не будет согласована с кабелем 50 Ом, в результате чего, в кабеле возникнут нежелательные стоячие волны, КСВ будет 100/50 = 2 и как следствие, потери передаваемой мощности, примерно 10%. Требуется рассчитать элементы согласования нагрузки с кабелем.
Для расчета, достаточно владеть основными навыками в алгебре.
Необходимо запомнить следующее правило:
При согласовании двух сопротивлений, элемент с большим сопротивлением, всегда будет трансформирован(преобразован) в элемент с меньшим сопротивлением, путем параллельного подключения к нему емкости.
Например:
Если мы имеем кабель 50 Ом и нагрузку 100 Ом, то нагрузка 100 Ом будет преобразована в сопротивление 50 Ом, путем подключения к ней параллельного конденсатора.
Иными словами, сопротивление можно только понизить, т.е привести к наименьшему из двух в данной цепи. В этом случае, всегда параллельно большему сопротивлению, будет включен конденсатор. Запомним это правило.
А теперь собственно сам расчет. Для лучшего усвоения, рассмотрим сначала более простую ситуацию, когда нагрузка не содержит реактивной составляющей, и согласовать надо только два чисто активных сопротивления(Рис.1)
Расчет состоит из пяти несложных шагов:
1. Рассчитаем коэффициент Q
Q = SQRT[(100/50)-1] = 1
2. Далее рассчитаем значение реактивности индуктивно(последовательной) ветви
ХL = Q x R1 = 1 х 50 = j50 Ом
3.Рассчитаем значение реактивности емкостной(параллельной) ветви
Хc = R2/Q = 100/1 = -j100 Ом
Знак минус – не результат вычислений, а для того, чтобы показать, что это емкостной реактанс.
Выберем рабочую частоту. Предположим, что мы согласуем два сопротивления для частоты 7 МГц( 7х10
6 Гц)
Тогда, зная значение индуктивной ветви, легко рассчитать саму индуктивность для заданной частоты
L = j50/(6.28 х 7х106) = 1.13мкГн
Емкость будет
С = 1/(6.28 х 7х106 х j100)= 227пФ
Знаки реактивности здесь не учитываются.
Теперь вспомним из раздела ,,Основы работы антенн,, что катушка и конденсатор имеют противоположные знаки реактивности. Если мы включим последовательно катушку и емкость, у которых реактивности равны по модулю на определенной частоте, т.е без учета их знаков, то в результате цепь не будет содержать никакого сопротивления. Наступит последовательный резонанс, резко возрастет ток в этой цепи, т.к. суммарное сопротивление на заданной частоте будет равно нулю.
Далее, для того чтобы понять ход
рассуждений, я сделаю небольшое
отступление в теорию. Обратимся к Рис.2, на
котором показана схема из двух
эквивалентных сопротивлений. 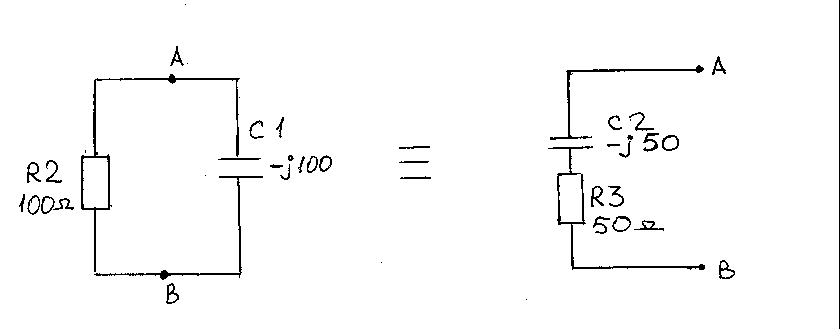
Рис.2
Если к резистору R2=100 Ом, параллельно подключить емкость C1= -j100, то эту схему можно полностью заменить эквивалентной схемой, у которой последовательно с резистором R3=50 Ом включена емкость C2= -j50. Иными словами, импеданс обеих схем, относительно точек А и В, будет абсолютно одинаковым. Это называется переводом параллельного импеданса в последовательный. Эту замену, можно производить с помощью программы tlcalc1.zip. Во втором разделе этой программы, можно переводить последовательный импеданс в параллельный и наоборот.
Далее, если мы теперь в схеме на Рис.1,
заменим нагрузку R2=100 Ом на параллельно включенные R2 и C1 из рисунка 2(слева), а затем заменим на эквивалентную схему R3 и C2, показанную на Рис.2( справа), то получим схему,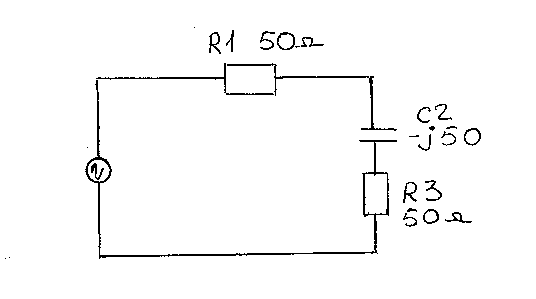
Рис.3
показанную на Рис.3.
В этой схеме мы замечаем, что имеем два одинаковых сопротивления R1 и R3, равные 50 Ом, и одну емкостную реактивность C2 -j50. Для ее компенсации, мы введем в схему индуктивную реактивность равную по значению С2. Поскольку, как мы уже знаем, катушка полностью нейтрализует емкость, т.к. имеет противоположный знак реактивного сопротивления. НаРис.4, у нас получилась согласованная схема, в которой остаются всего два равных резистора 50 Ом. Реактивности L1 и C2 взаимно уничтожаются, о чем уже говорилось выше.
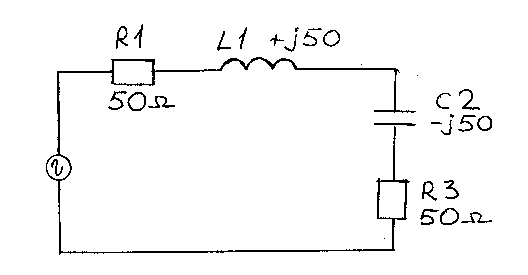
Рис.4
Теперь осталось пройти последний шаг. Поскольку мы заменяли сопротивление R2=100 Ом и параллельно включенный ему конденсатор C1=-j100(Рис.2, слева) на последовательный эквивалент R3 и C2(Рис.2 справа), возвратимся к исходной нагрузке, поскольку, исходное сопротивление нагрузки равно 100 Ом. Полученная схема показана на Рис.5.
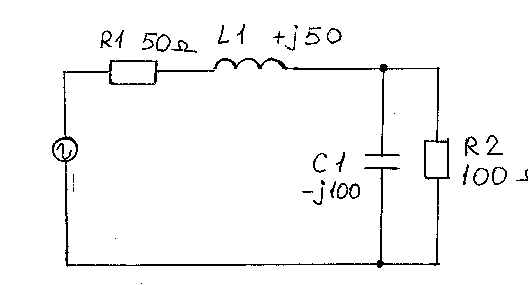
Рис.5
Окончательная схема согласования приводится на Рис.6, и обведена пунктиром. Итак, мы имеем нагрузку 100 Ом, и два согласующих элемента С1 и L1.
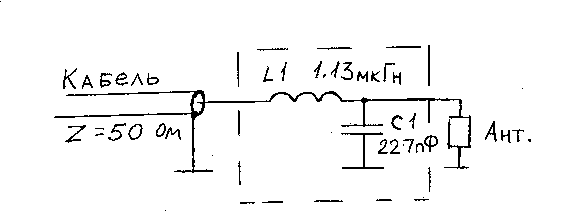
Рис.6
В расчете, который мы произвели выше, мы определили значения емкости и индуктивности для частоты 7 Мгц. Подставляем эти значения в схему.
Обратите внимание, что параллельный конденсатор в схеме оказался у того конца, на котором большее сопротивление.
Отступление мною делалось для того, чтобы читатель понял, почему в конечной схеме появляется индуктивность.
Рассмотрим для практики еще один пример:
Кабель 75 Ом питает антенну(нагрузку) 25 Ом(Рис.7) В этом случае, нагрузка R2 меньше сопротивления кабеля R1.
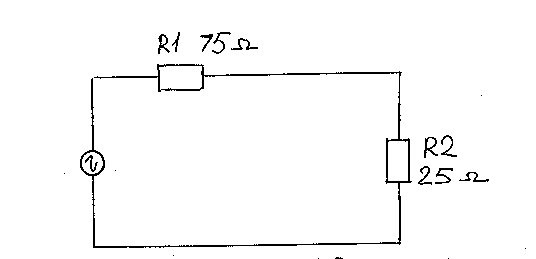
Рис.7
Рассчитаем схему согласования для 14 МГц.
Рассчитаем коэффициент
Q = SQRT(75/25)-1 = 1.41
Индуктивная реактивность
ХL = 25 x 1.41 = 35.25 Ом
Емкостная реактивность
ХС = 75/1.41 = 53.19 Ом
Индуктивность для 14 МГц
L = 0.4 мкГнЕмкость
C = 213.7 пФ
Схема с расчетными елементами показана на Рис.8.
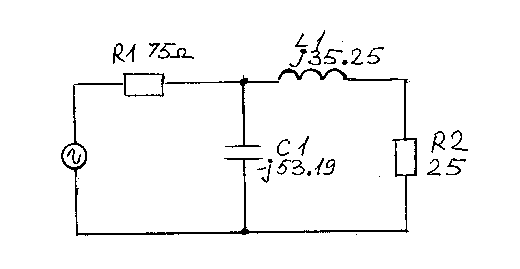
Рис.8
На Рис.9, показана окончательная схема согласующего устройства, обведенная пунктиром.
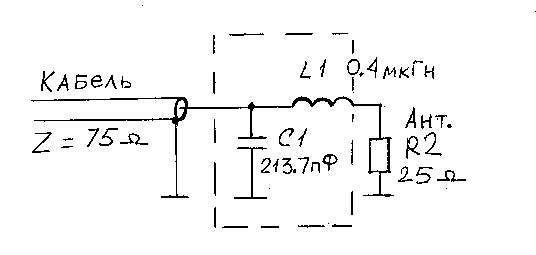
Рис.9
Мы видим, что параллельный конденсатор оказался подключенным параллельно большему сопротивлению R1, в данном случае - кабелю. Как вы обратили внимание, расчет точно такой же, только емкость подключена уже не к нагрузке, а к кабелю, поскольку он имеет большее сопротивление в данной цепи, т.е. все преобразования теперь производятся с сопротивлением 75 Ом(сопротивление кабеля), поскольку оно наибольшее в данной цепи.
Это правило надо запомнить хорошо, чтобы в дальнейшем не возникало ошибок при согласовании нагрузок.
Мы разобрали способ согласования нагрузки с источником. Все сопротивления были чисто активными, т.е. не имеющими никакой реактивной составляющей. На практике, такие ситуации встречаюся значительно менее часто, чем те, когда мы имеем комплексную нагрузку, которую необходимо согласовать с активным сопротивлением(кабелем). Строго говоря, если учесть, что кабелей без потерь не существует, волновое сопротивление кабеля не является чисто активной величиной, и всегда содержит хоть и очень незначительную, но комплексную составляющую. Как же согласовать комлексные сопротивления?
В следующем разделе мы рассмотрим примеры согласования комлексных нагрузок.
Согласование импедансов, содержащих реактивную составляющую.
Сразу надо отметить, что расчет согласующих элементов для нагрузки, содержащей реактивность, почти не отличается от предыдущего расчета.
Следует запомнить еще одно правило для этого случая:
Расчет начинается с того, что мы мысленно игнорируем, не учитываем все реактивности согласуемой цепи, и производим расчет, как для случая с чисто активными сопротивлениями.
Поясню все на примере.
Кабель R1 50 Ом, имеет комплексную нагрузку, состоящую из последовательно включенных R2 и C1. Импеданс нагрузки:
Z=25 -j10 Ом
Поскольку величины сопротивления кабеля и нагрузки - разные, необходимо расчитать согласующие элементы.
Рассматриваемая схема, представлена на Рис.10. Мы видим, что нагрузка кабеля - R2 и C1, имеет емкостную составляющую -j10.
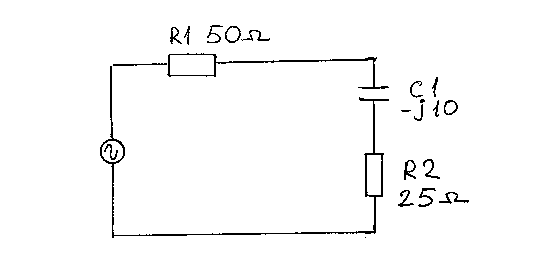
Рис.10
Рассчитаем элементы согласования, не учитывая реактивность -j10, т.е. как для случая с чисто активными элементами, рассмотренного в предыдущем разделе. Не забываем, что в данном случае кабель имеет большее сопротивление, и следовательно параллельный конденсатор следует подключить именно параллельно кабелю.
Рассчитанные значения элементов согласования для этого случая показаны на Рис.11.
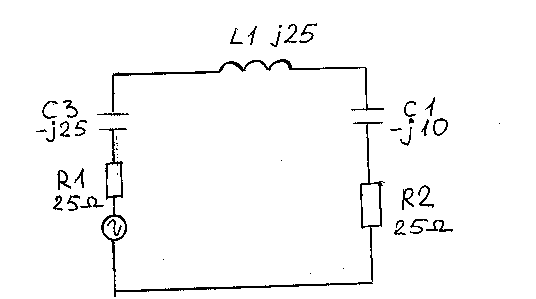
Рис.11
Мы уже знаем, что сопротивления R1=50 Ом(кабель), преобразовано в сопротивлениеR1=25 Ом плюс последовательная емкостьC3=-j25, т.е.в последовательный эквивалент. Индуктивность L1=j25 компенсирует реактивность C3.
На Рис.12, показана схема, на которой последовательное соединение R1 и C3(Рис.11), заменено параллельным эквивалентом R1 и C2(Рис.12).
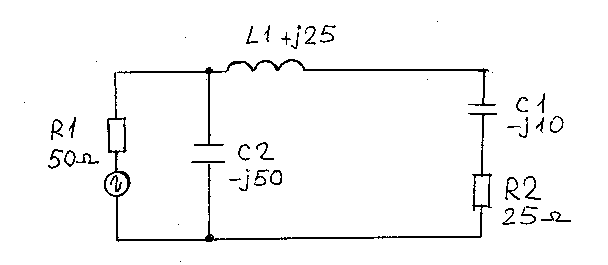
Рис.12
Мы видим, что схема содержит два одинаковых сопротивления 25 Ом. Остается некомпенсированной только лишь одна реактивность C1=-j10. Что мы должны сделать в этом случае? Оказывается все очень просто! Реактивность C1=-j10, мы компенсируем добавлением к имеющейся нидуктивной реактивности, дополнительно +j10, т.е. попросту увеличиваем индуктивную реактивность. В результате всего этого, мы будем иметь схему согласования, показанную на Рис.13.
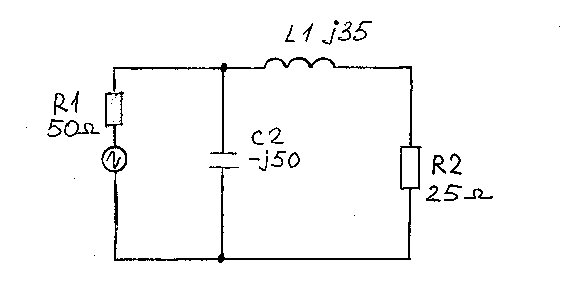
Рис.13
Осталось, для реальности, рассчитать значения элементов для конкретной частоты, т.е перевести реактивности в значения емкости и индуктивности.
Предположим, что нас интересует частота 21 МГц.
Тогда:
L1 = 0,265 мкГн
C1 = 151,6 пФ
На Рис.14, показана реальная схема согласования.
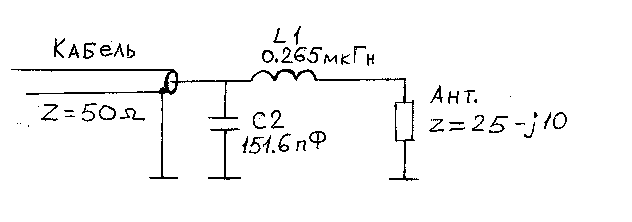
Рис.14
Все расчеты по согласованию импедансов не слишком сложны, поэтому после нескольких тренировочных расчетов, можно предположить, что многие смогут освоить эти, столь нужные вычисления.
Хочу отметить, что описанные оба способа расчета элементов согласования кабеля с антенной, справедливы не только в этих случаях. По этим правилам, можно также расчитать элементы согласования, если вы согласуете усилитель ПЧ с кварцевым фильтром, или два каскада постоянной ПЧ. Для этого необходимо знать выходное сопротивление каскада и входное сопротивление следующе