Теоретическое доказательство существования нового представления о распространении радиоволн"

После публикации мною трех статей на этом сайте в разделе «Непроверенные идеи» было получено много отзывов, в том числе и упреков в дилетантстве. Тот факт, что читающих статьи оказалось очень много (порядка 3,5 тысяч) свидетельствует об интересе к этой теме. Для завершения рассмотрения этого вопроса мне необходимо привести те соображения, которые легли в основу публикаций, ибо как я понял, молодые радиолюбители и даже достаточно опытные просто не в курсе дела. Мне 77 лет, я КТН, доцент Тольяттинского госуниверситета. Мною опубликовано свыше 120 научных статей и четыре книги научного содержания по отдельным проблемам. Так, что я далеко не дилетант в науке. Конечно в области радиолюбительства я, как и все увлекающиеся этим, занимался на досуге. Конечно, по своему уровню знаний, я кое-что делал и в области теории радиоэлектроники, например, разбирался в действии согласующих устройств, но не публиковал это, а с успехом использовал сам. Считаю обязанным довести до сведения широкого круга радиолюбителей о противоречиях, в теории распространения радиоволн, чтобы новое поколение знало об этом и продолжило изыскания в этой области. Это касается так называемого дальнего поля, где, как видно из моих публикаций есть основание для изменения существующих представлений. Вообще электромагнитной теории распространения света предшествовала корпускулярная теория, то есть распространения в виде некоторых частиц. Новое представление возникло с созданием системы уравнений Максвелла для электромагнитных колебаний.

(а), (b) (1)

(с), (d)

Для тех, кто неискушен в символах высшей математики, можно пояснить, что уравнение (1b) представляет собой закон индукции Фарадея. Правая часть этого уравнения определяет изменение напряженности магнитного поля по времени . Это изменение вызывает появление электрического вихревого поля , что выражается левой частью этого уравнения (). В уравнении (1a) последний член, при отсутствии тока, что имеет место при распространении радиоволн в вакууме, равен нулю. Первый член правой части (1а) определяет изменение напряженности электрического поля в зависимости от времени. Это изменение приводит к появлению вихревого магнитного поля (). Величина , в правой часть двух уравнений, постоянна и равна скорости распространения света. Собственно эти уравнения определили, что должны существовать электромагнитные колебания в виде радиоволн, хотя опытным путем их, до получения этих уравнений, еще никто не обнаружил. Это было сделано позже. Так вот, вскоре, после появления системы уравнений электромагнитных колебаний было предложено два простейших варианта их решений. Один из них, более удобный для анализа, дается двумя уравнениями

(а), (b) (2)

(c), (d).

Здесь: и - максимальные значения напряженностей электрического и магнитного полей; - длина волны. Уравнения (2) здесь приведены в несколько измененной форме, привычной сейчас для радиолюбителей. Но суть изменений совершенно не коснулась природы этих уравнений, записанных ранее в безразмерной форме. Выбор этих зависимостей еще определяется тем, что они выражают бегущую волну, при которой передается энергия. Так вот, если подставить уравнения (1а) и (1b) в систему (1), то обнаружится тождество, при условии . Это означает, что выражения (2) являются частным решением системы (1). После этого было проведено множество аналитических исследований с применением комплексных переменных и векторного анализа. Но, во всех случаях, основная ориентировка велась на решения (2), которые и сейчас остались основными, по которым можно судить о природе распространения радиоволн. Рассмотрим, что же представляют собой эти решения. Прежде всего, обращает внимание тот факт, что электрические и магнитные поля совпадают по фазе во времени и по координатам. Это означает, что оба поля одновременно увеличиваются или уменьшаются, имея одинаковый знак. Если как бы зафиксировать время, допустим условной фотографией, то распределение полей будут выглядеть, как представлено на рис. 1

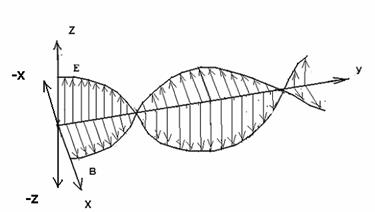
Рис. 1. Схема распределения полей по длине в какой-то момент времени по существующим представлениям.

Как видно здесь имеются точки, где значения полей равно нулю. Это означает, что энергия передается порциями. Если рассматривать какое-либо сечение по оси , то в результате оба поля будут изменяться по закону косинусу. Причем будут моменты, когда оба поля окажутся равными нулю, то есть они исчезнут и, затем вновь появляются. Если, допустим, наблюдатель будет двигаться со скоростью света, вместе с распространяющимися полями, то есть при условии , то он может обнаружить застывшие поля, в зависимости от фазы, с которой началось движение. То есть это действительно распространение, наподобие волн на воде. Более того, еще где-то 40 лет назад мною, при анализе уравнений (1а,b) было установлено, что решения (2) не удовлетворяют им по так называемым функциональным граничным условиям. Что это поясню следующим образом. Подставим уравнения (2) в (1а).

(а), (3)

(b)

Как видно здесь правые части равны, что свидетельствует о том, что (2) удовлетворяют первому уравнению Максвелла (1а). Рассмотрим частный случай, когда и . Подставляя эти значения в (2) и вспоминая, что косинус нуля равен единице, получим и . Это означает, что в этой точке электрические и магнитные поля максимальны. Из (3а), после подстановки выбранных условий, следует . Это известное условие экстремума, то есть точки максимума или минимума напряженности электрического поля, что как раз следует из (2). Соответственно из (3b) следует . Это означает, что индуцированное магнитное поле отсутствует. Но, мы только что получили, что оно максимально . Еще более показателен случай , что дает , . То есть здесь есть противоречие. Конечно, можно много рассуждать, объясняя это обстоятельство, вплоть до того, что приходится признавать сами уравнения Максвелла как аксиому, то есть истину, принимаемую без доказательств, не исключая, а увеличивая сомнения. В принципе это результат свидетельствует, что бегущая волна в форме (2) не удовлетворяет уравнениям Максвелла по функциональным условиям. Когда появились портативные радиостанции, и выяснилось, что имеются точки, где пропадают сигналы, как описано в моих статьях, то и возникло предположение, что в дальнем фронте существуют какая-то другая форма распространения. Опыты с установкой дополнительных боковых рефлекторов, подтвердили это предположение, хотя для этого потребовалось довольно большие усилия. Конечно, критиков, выдвигавших другие варианты объяснений, было предостаточно. Основные возражения были большей частью по поводу моего дилетантства, выражающегося в «покушении» на уравнения Максвелла и широко принятый вариант объяснения распространения радиоволн в дальнем фронте, как показано на рис. 1, хотя нарушения уравнений Максвелла, наоборот, касались как раз существующих представлений. Чтобы завершить дискуссию, конечно же, надо было бы попробовать получить какое-либо другое решение уравнений Максвелла, которые были бы лишены отмеченных сомнительных моментов. С помощью продолжившейся по E-Male дискуссии с одним из ее участников Андроповым Е. В. выяснилось, что другого пути просто не просматривается. Конечно, эта задача весьма сложна, но, как-то повезло и удалось предложить новый вариант решения в виде

(а), (b) (4)

, , (с).

Это решение в какой-то степени, разложением по координатам, похоже на (2), но здесь решение искалось в виде произведения двух функций, одна из которых зависит от времени, другая – от координат. Подставим эти значения в правую и левую части (1а).

(а) (5)

(b)

Как видно левая и правая части равны, что свидетельствует о том, что и выражения (4) удовлетворяют уравнениям Максвелла.

Рассмотрим участок, где , . Подставляя эти значения в (4), (5а,b) получим . Это условие того, что рассчитываемое электрическое поле находится в точке максимума или минимума. Из (4а) действительно следует . То есть это действительно максимальное значение, хорошо увязываемое со значением производной. Далее, из подстановки выбранных условий следует для левой части уравнения . Это означает, что индуцированного магнитного поля нет. Это как раз подтверждается (4b) . Таким образом, здесь нет того противоречия, которое наблюдается в решении (2). Если провести всю процедуру подстановок в уравнение (2 b), то и здесь также, в отличие от решения (2) здесь также не обнаруживаются какие-либо противоречия. Но, увы, уравнения (4) определяют так называемую стоячую волну, при которой, по классическому определению нет передачи энергии. На это обратил внимание ДТН Федосеев О. Б., при обсуждении проблемы. Правда, выражения (4), не соответствуют, стоячим волнам, которые получаются от наложения прямой и отраженных волн, ибо они описываются как произведение синуса на косинус. Но, в таком случае, если выражения для них подставить в уравнения Максвелла, то они им, увы, не удовлетворяют.

Как видно поиск логического решения модельной одномерной задачи и здесь встретил затруднения. Не достает еще какого-то условия для логического продолжения. Работа в этом направлении привела к проверке эффекта от наложения полей (4), отражающее совместное действие электрических и магнитных полей в виде суммы уравнений (4). Как оказывается, в этом случае получается бегущая волна при условии .

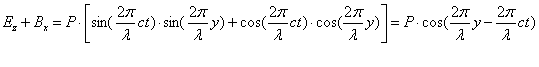(7)

То есть в таком представлении отдельно ни электрическое поле, ни магнитное поля, образуемые стоячими волнами, энергию не передают, а их взаимодействие образует бегущую радиоволну, с передачей энергии. То есть передача энергии электромагнитных колебаний происходит взаимодействием двух стоячих волн специфического вида (4). Этот результат многому обязывает по дальнейшей расшифровке природы распространения радиоволн. Причем правая часть (7) вовсе не говорит, что с чего начали - (2) к тому и пришли – (7). Здесь просто доказывается, что такие стоячие волны, при взаимодействии способны передавать энергию. Собственно говоря, понятие о дальней зоне возникло именно из первого решения (2). Теперь оно теряет смысл, ибо решение (4) описывает как ближнее поле, так и дальнее поле. Посмотрим, что себе представляют решения (4). Во-первых, здесь электрические и магнитные поля находятся в разной фазе. На всем протяжении по оси существуют точки, , где есть только электрическое поле и точки, , где будут только магнитные поля. Здесь последовательность целых чисел. На всем протяжении оси происходят колебательные процессы обмена энергии электрических и магнитных полей. Если наблюдатель будет двигаться совместно со скоростью распространения колебаний, то есть, , то, в отличие от (2), он увидит поля, изменяющиеся по времени, что вполне естественно для колебательного процесса. Такой схемой полностью объясняется эффект лазерного излучения. Все, что излагалось в предыдущих статьях, как догадка, находит в этой модели подтверждение. Диаграмма распределения полей по продольной координате выглядит следующим образом

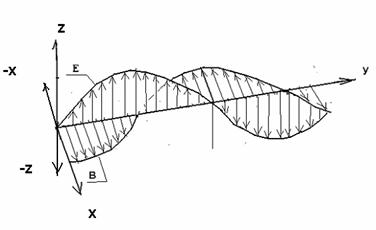
Рис. 2 Диаграмма распределения полей по уравнениям (4).

Теперь получается, что было бы даже странным, что пропадания сигнала на 144 мгц, при перемещении портативной станции, что поголовно наблюдают радиолюбители, могли бы отсутствовать, ибо из (4) следует, что как такового фронта распространения радиоволн нет, а есть отдельные кольцевые, взаимосвязанные электрические и магнитные вихри. Они то и образуют поле в виде кольчуги, распространяясь в виде деления на вихри меньшей мощности в радиальном направлении

В заключении выражаю благодарность всем читателям моих статей, критиков, даже со слишком поспешными оценками моей личности. Конечно, я не знал, что на протяжении 40 лет так и не было подвергнуты сомнению уравнения (2). Теперь, появление решения (4), дает к этому новый импульс. На последнем семинаре по обсуждению новых обстоятельств, в структуре распространения радиоволн, которые изложены здесь, были высказаны соображения о больших последствиях в деле объяснения биологического воздействия света. Интересно, сколько времени потребуется, чтобы были осмыслены и сопоставлены уравнения (2) и (4)? Представляется, что среди радиолюбителей есть много студентов и преподавателей этого профиля. Использование материалов данной статьи может послужить основой для широкого обсуждения и различного вида более подробных и более сложных расчетов. Советую скопировать статью и использовать ее в дальнейшем. Конечно же, интересуюсь вашим мнением и дальнейшим обсуждением.

Теоретическое доказательство существования нового представления о распространении радиоволн

Автор: Ляхов В. К. UA4HUL