Щелевая и копланарная линии
Щелевая линия (ЩЛ) (рис. 1.12) представляет собой узкую щель в проводящем слое, нанесенном на поверхность тонкой диэлектрической подложки. Другая поверхность подложки остается свободной от покрытия.
При использовании ЩЛ энергия излучения должна быть минимальной. Это достигается применением подложек с высоким значением е (е>10), что приводит к значительному уменьшению длины волны Л в линии.
Потери на излучение сводятся к минимуму, а поле концентрируется вблизи щели. Применение экрана исключает потери на излучение.
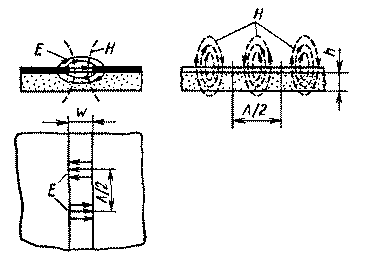
Рис. 1.12. Общий вид щелевой линии и структура поля низшей волны
На рис. 1.12 показано распределение поля в ЩЛ. Электрические силовые линии направлены перпендикулярно щели. Благодаря этому создается возможность удобного и простого присоединения параллельно линии внешних сосредоточенных элементов (резисторов, конденсаторов, диодов и др.). В плоскости симметрии линии, проходящей через щель перпендикулярно подложке, магнитные силовые линии образуют замкнутые петли с периодом в половину длины волны. Поэтому в ЩЛ имеются области эллиптической поляризации магнитного поля, что можно использовать при создании невзаимных ферритовых устройств. Важной особенностью ЩЛ является также и то, что она используется в комбинации с микрополосковой линией, нанесенной с другой стороны той же подложки, при создании объемных интегральных схем и устройств СВЧ. При строгом электродинамическом анализе ЩЛ может быть применен тот же подход, что и в случае МПЛ, который описан подробно в предыдущем параграфе. Расчетная модель ЩЛ (рис. 1.13) представляет собой подложку (область 2) со слоем металлизации, ограниченную экраном прямоугольной формы. Наличие электрической стенки в плоскости х=0 соответствует основному типу волны ЩЛ. Области / и 3 имеют, как правило, воздушное заполнение.
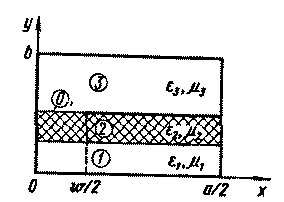
Рис. 1.13. Расчетная модель экранированной ЩЛ (поперечное сечение)
Применяя рассмотренную в § 1.1 методику к модели рис. 1.13, можно получить дисперсионное уравнение экранированной ЩЛ, подобное соотношению (1.18), и рассчитать волновое сопротивление ЩЛ. Частотные зависимости коэффициента замедления р и волнового сопротивления Z0 для волны основного типа экранированной ЩЛ, полученные указанным методом, представлены на рис. 1.14. Как видно из рисунка, с ростом частоты наблюдается снижение волнового сопротивления и рост коэффициента замедления волны в ЩЛ. Сужение щели приводит к уменьшению Z0 и повышению р.
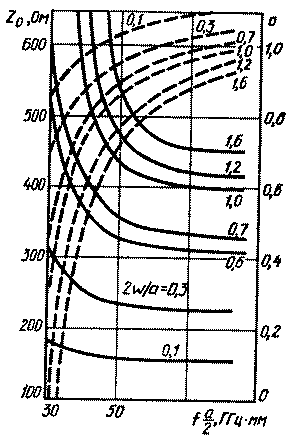
Рис. 1.14. Частотные зависимости коэффициента
замедления р (- - -) волнового сопротивления Zo (---) экранированной ЩЛ
Практический интерес представляют сравнительные данные по характеристикам ЩЛ и МПЛ при их одинаковой геометрии и достаточном удалении экрана. На рис. 1.15 показана зависимость волнового сопротивления обеих линий от параметра w/h. Как видно из рисунка, при одинаковой геометрии линий большие значения волнового сопротивления легче реализовать в ЩЛ. Однако, как показывают расчеты, МПЛ имеют большее значение р, а их дисперсия выражена значительно слабее, чем у ЩЛ. Потери на единицу длины линий обоих типов одного порядка.
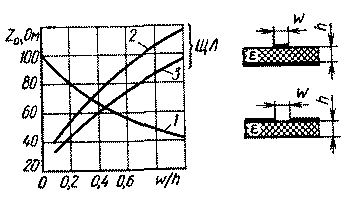
Рис. 1.15. Сравнительная оценка волновых сопротивлений МПЛ и ЩЛ для е=16:
1— МПЛ; 2 —ЩЛ при f=1,7 ГГц; 3 — ЩЛ при f=5,4 ГГц
В настоящее время все более широкое применение находят несимметричные ЩЛ, позволяющие легко реализовать практически любое волновое сопротивление, проектировать схемы с двусторонней топологией, а также осуществлять переход на линии других типов. На рис. 1.16 приведены дисперсионные характеристики основной волны и первых трех высших типов волн несимметричной МПЛ. Как видно из графика, все типы волн обладают низкочастотной отсечкой. При Л->0 дисперсионные характеристики волн всех типов стремятся к значению Ve. Характер дисперсионных зависимостей показывает, что несимметричные ЩЛ можно отнести к линиям передачи волноводного типа. Полоса одноволнового режима ЩЛ равна аналогичной полосе прямоугольного волновода. При длинах волн за точкой отсечки постоянные распространения всех типов волн становятся мнимыми.
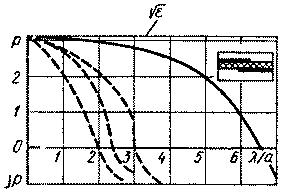
Рис. 1.16. Дисперсионные характеристики волн низшего ( — )
и высших (- - -) типов экранированной несимметричной ЩЛ
Копланарная линия представляет собой трехпроводную по-лосковую линию передачи, в которой электромагнитная волна распространяется вдоль щелей между полосковыми проводниками, расположенными в одной плоскости. Средний проводник является токонесущим, а два крайних — «заземленными» (рис. 1.17). Вся система проводников расположена на однослойной диэлектрической подложке или на многослойной подложке из разных материалов.

Рис. 1.17. Копланарная линия.
Копланарную линию можно считать разновидностью ЩЛ. Как и щелевая, копланарная линия не имеет нижней частоты отсечки, и в ней используются подложки с высокой диэлектрической проницаемостью в, что обеспечивает значительное уменьшение длины волны в линии и концентрацию электромагнитного поля вблизи границы раздела диэлектрик — воздух.
На копланарной линии удобно располагать внешние сосредоточенные элементы при разработке гибридных интегральных схем. Магнитное поле на поверхности подложки эллиптически поляризовано, что позволяет создавать на линии, нанесенной на ферритовую подложку, различные невзаимные устройства. Заземленные пластины можно соединить металлической перемычкой, которая служит одновременно и экраном (рис. 1.18). Вследствие концентрации поля вблизи подложки такой экран не вносит искажений, если он удален не менее чем на расстояние 4b от подложки.
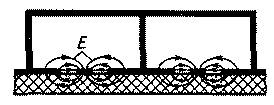
Рис. 1.18. Экранированные копланарные линии
Расчет экранированной копланарной линии может быть осуществлен методам, частичных областей. Уравнения Гельмгольца решаются в области поперечного сечения экранированной копланарной линии. Граничные условия накладываются на поля в плоскости частично металлизированной поверхности копланарной линии. Разложениие полей на этой поверхности, рассматриваемой как вырожденная область, выполняется по системам базисных функций, удовлетворяющих условиям Мейкснера на кромках полосковых проводников (например, по полиномам Чебышева или по функциям Бесселя полуцелого порядка). В продольной плоскости симметрии линии располагается магнитная стенка, что позволяет решать задачу только в одной части линии, распространяя затем решение на вторую ее часть. Удовлетворяя граничным условиям на частично металлизированной поверхности линии, можно получить дисперсионное уравнение и исследовать спектр собственных типов волн в линии.
Результаты расчета коэффициента замедления и волнового сопротивления копланарной линии приведены на рис. 1.19.
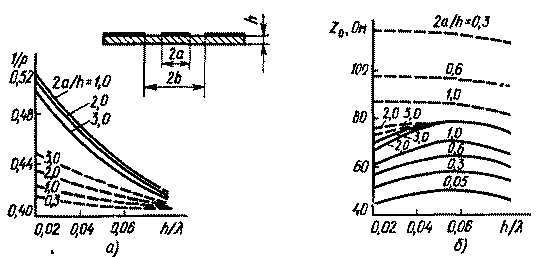
Рис. 1.19. Частотные зависимости коэффициента замедления (а) и волнового
сопротивления (б) коплаиариой линии: ---- четный тип; - - - нечетный тип
Расчеты показали, что в копланарной линии существуют два основных типа колебаний (четный и нечетный типы), отличающиеся распределением электромагнитного поля. В случае колебания четного типа крайние и центральный проводники находятся под разными потенциалами. При нечетном типе колебания крайние проводники имеют один потенциал, а центральный проводник — другой. Распределение электромагнитного поля в этом случае показано на рис. 1.18. Как видно из рис. 1.19, колебания четного и нечетного типов имеют разные коэффициенты замедления и волновые сопротивления. С ростом частоты наблюдается рост р, а значение Z0 изменяется мало.