ПPOCTO ОБ АНТЕННАХ, ИЛИ ИЗМЕРЯЕМ КСВ
В.Башкатов, US0IZ, г.Горловка, Донецкой обл.
Поскольку радиолюбитель является разработчиком антенно-фидерных устройств (АФУ) своей радиостанции, он должен ясно представлять себе явления, происходящие в них. Важнейшим показателем, по которому с определенной степенью точности можно судить о фактической эффективности АФУ, является коэффициент стоячей волны (КСВ). Практически все коротковолновики знают, что при настройке АФУ следует стремиться к "заветной" единице и не выходить за некоторые граничные значения КСВ. Как указывалось в [1], для передачи высокочастотной энергии от передатчика к антенне используют фидерные линии (или просто фидеры). Радиолюбители, как правило, в качестве фидеров применяют коаксиальные линии, и реже - двухпроводные симметричные линии. Одиночные фидерные линии в настоящее время практически не применяются, т.к. они создают нежелательные потери при излучении и могут быть причиной помех устройствам, вблизи которых проходит такой фидер. Хотя 50...70 лет назад среди радиолюбителей-коротковолновиков весьма популярной была Т-образная антенна под названием "американка", используемая при работе с передатчиком, имеющим несимметричный (однотактный) каскад, и питаемая одиночным фидером. Если длина фидера не превышает одной десятой рабочей длины волны (O.U), с небольшим приближением его можно считать простым соединительным проводом, не создающим каких бы то ни было специфических проблем при передаче энергии. Однако на практике не все радиолюбители живут на верхнем этаже многоэтажного дома или имеют возможность установить свой трансивер рядом с антенной в частном доме. Если на низкочастотных КВ-диапазонах (160 и 80 м) использование короткого фидера еще иногда возможно, то на остальных КВ-диапазонах (40...10 м) такой возможности, как правило, нет. Таким образом, на практике длина фидера может составлять десятки метров, и такой длинный фидер (сравнимый с длиной волны) при определенных условиях (например, если КСВ в нем отличен от 1) "проявляет свой норов" и создает проблемы владельцу радиостанции. Однако КСВ=1, как правило - редкое явление. Характеристическое (или волновое) сопротивление коаксиального фидера обычно составляет 50 или 75 Ом (хотя отечественная промышленность производит и другие коаксиальные кабели, например, на 100 и 150 Ом, но на практике они применяются редко). Значение волнового сопротивления фидера, изготовленного в виде двухпроводной линии, лежит в пределах 200...600 Ом. При этом необходимо отметить, что волновое сопротивление фидера Z целиком зависит от его геометрии и диэлектрической постоянной материала изоляции и выражается следующими формулами: - для двухпроводной линии:
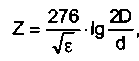
где d - диаметр проводников линии, D - расстояние между проводниками; - для коаксиального кабеля:
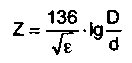
где d -диаметр внутреннего проводника, мм, D - диаметр внешнего проводника (оплетки), мм, е - диэлектрическая постоянная материала изоляции между проводником и оплеткой (для полиэтилена е = 2,3). В первой части статьи [1] было показано, что "физическая" (т.е. измеряемая рулеткой) и "электрическая" (т.е. с учетом свойств кабеля при распространении в нем электромагнитной энергии) длины одного и того же отрезка коаксиального кабеля разные. Это значит, что отрезок такого кабеля длиной 4,1 м на частоте 24 МГц (длина волны l=300/f=12,5 м) ведет себя как полуволновой повторитель с электрической длиной 6,25 м. Для воздушного фидера "физическая" и "электрическая" длины совпадают. Далее рассмотрим (рис.1а) различные случаи, которые могут возникнуть в системе передатчик-фидер-нагрузка при различных видах и вариантах нагрузки. Представим схематично, что передатчик (источник сигнала e(t) с выходным сопротивлением R,.) через фидер с волновым сопротивлением Rф подключен к антенне, т.е. к нагрузке с полным комплексным сопротивлением (или иначе импедансом) Z„ или с сопротивлением R„ (если нагрузка чисто активная). Известно, что передача высокочастотной энергии по фидеру происходит вследствие распространения вдоль него электромагнитного поля, поэтому рассмотрим процессы, происходящие в кабеле при распространении простейшего импульсного сигнала. До момента времени t.i в линии нет никакого напряжения. Допустим теперь, что в момент времени t^ на входе линии в точках а и б произойдет скачкообразное появление постоянного напряжения Е (рис.16), которое далее остается неизменным. Т.к. сигнал не может мгновенно распространяться по проводам, то в момент времени t.i разность потенциалов между проводами линии (справа от входа) все еще равна нулю. Далее, разность потенциалов Е, возникшая в начале линии, начнет распространяться по ее проводам со скоростью примерно 200 000 км/с, или 200 м за 1 мкс (U., на рис.16). Эта прямая волна через некоторое время (в момент Ц ) достигнет конца линии (U^ на рис.1 в). Здесь возможны три характерных случая: - если сопротивление нагрузки очень велико, т.е. R^ -> °° (бесконечность), эта волна напряжения имеет единственный путь для дальнейшего распространения - повернуть обратно и пойти по тем же проводам (Uy на рис.1 г). При этом происходит удвоение потенциала между проводами, так как в прямом направлении линия продолжает питаться источником напряжения; - если линия короткозамкнута на конце (1)4 на рис.1д), т.е. Рц = 0, волна продолжает свое распространение в обратном направлении по тем же проводам, но "поменяв" их местами (ток одного провода продолжает свой путь по другому проводу, так как для этого есть короткозамкнутая перемычка). В этом случае произойдет нейтрализация разности потенциалов,так как полярности прямой и обратной волны противоположны; - имеется такое сопротивление R^ = R^rn (между RH = 0 и RH -> °°), при котором волна, дойдя до правого конца линии, поглощается нагрузкой и не возвращается назад (Ug на рис.1е), при этом разность потенциалов между проводами линии остается неизменной. Это сопротивление называют волновым или согласованным. Пусть в момент 1д на линию поступает синусоидальный сигнал Ugg (рис.1ж). Волна от этого фронта сигнала начнет распространяться по линии и через некоторое время окажется в точке b (UL на рис.1з) Левее этой точки распределение потенциалов в линии (по ее длине) соответствует течению входного процесса во времени (это соответствие показано стрелками на рис.1з). Когда волна дойдет до правого конца линии, то, в зависимости от характера нагрузки, также могут быть три случая: - если линия разомкнута, волна вернется обратно, взаимодействуя при этом с продолжающейся двигаться в право прямой волной. Эта обратная волна будет то складываться с прямой волной, то вычитаться из нее. В некоторых точках линии напряжение всегда будет равно нулю (узлы напряжения), а в некоторых точках амплитуда напряжения будет максимальна (пучность напряжения).
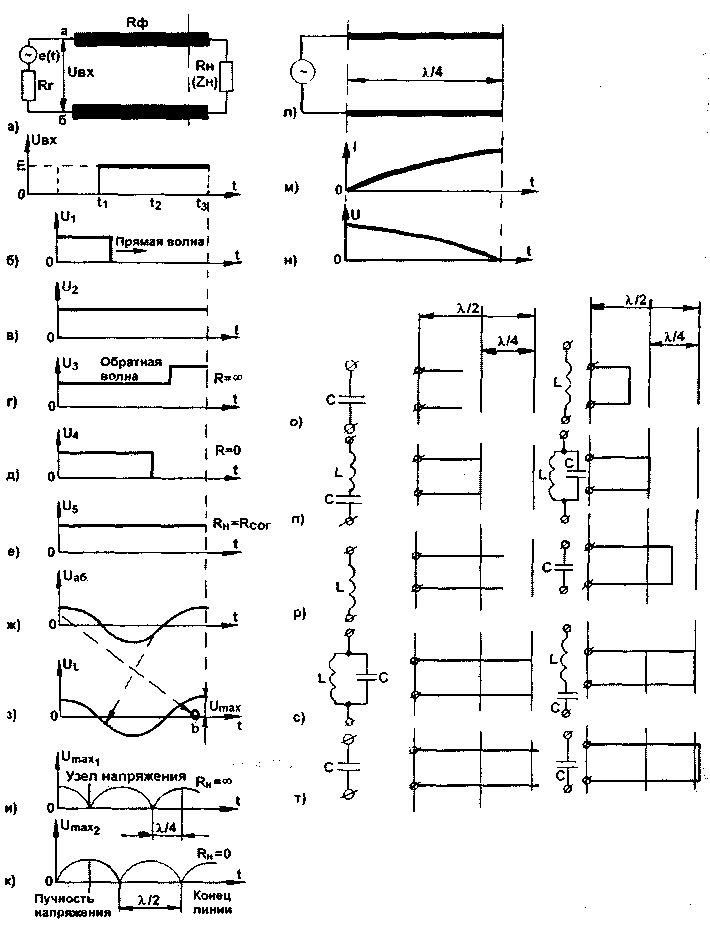
Рис. 1
Для разомкнутой линии (Umax1 на рис.1и) распределение амплитуд (а не мгновенное значение, как на рис.1з) таково, что на конце линии всегда пучность напряжения и узел тока, а для короткозамкнутой (Umax2 на рис.1к) на конце всегда узел напряжения и пучность тока (рис.1м). Это явление широко используется в УКВ-технике для создания колебательных систем на отрезках линий (рис.1л). На рис.1о...т показано такого рода соответствие для ряда отрезков замкнутых и разомкнутых линий. В случае разомкнутой линии на расстоянии четверти длины волны l/4 от конца разомкнутой линии всегда образуется узел напряжения (кривая Umax1)- Такая линия эквивалентна по своим свойствам последовательному колебательному контуру, сопротивление которого минимально при резонансе (фильтр-шунт). При этом на входе линии получается максимум тока и минимум напряжения. Разомкнутая линия длиной меньше четверти длины волны (l<l/4) имеет емкостное входное сопротивление, т.е. эквивалентна емкости, подсоединенной к входным зажимам. При l>l/4 входное сопротивление становится индуктивным, и при длине, равной l/2, разомкнутая линия эквивалентна параллельному колебательному контуру, имеющему максимальное сопротивление при резонансе (фильтр-пробка). В этом случае на входных клеммах наблюдается максимум напряжения и минимум тока. Для уменьшения размеров таких линий можно применить удлинительные емкости или индуктивности, подключение которых заменяет удаленные отрезки линии. - в случае короткозамкнутой линии той же длины, что и разомкнутая, картина меняется на обратную. То, что происходит на конце кабеля, который подключен к нагрузке, зависит от характера нагрузки. Если полное сопротивление нагрузки носит чисто активный характер (т.е. она не имеет индуктивной или емкостной составляющей) и по своему значению равно волновому сопротивлению фидера, никаких проблем не возникает Электромагнитная волна благополучно "пробежит" от передатчика к нагрузке, и перенесенная ею электромагнитная энергия вся целиком "уйдет" в нагрузку - рассеется в нагрузочном резисторе или излучится в эфир (если нагрузка - входное сопротивление антенны). Эту электромагнитную волну принято называть падающей. Если измерять распределение напряжения и тока вдоль фидера, окажется, что они имеют постоянные значения на всей его длине (рис.2г для случая Rн=Рф). Строго говоря, последнее справедливо лишь для фидера без потерь. Ситуация, когда нагрузка носит чисто активный характер и имеет такое же сопротивление, равное волновому сопротивлению фидера, на практике встречается крайне редко. Обычно имеет место несовпадение этих сопротивлений и/или наличие у нагрузки не только активной, но и реактивной составляющей. Причем, чаще всего наблюдается и рассогласование по активной нагрузке, и наличие реактивности. Мерой степени рассогласования фидера с нагрузкой служит коэффициент стоячей волны (КСВ). Если идеального согласования фидера с нагрузкой нет, то часть высокочастотной энергии не поступает в нагрузку (отражается от нее), и в фидере начинает распространяться электромагнитная волна в обратном направлении - к передатчику. Эту волну называют отраженной. Мощность, отраженная от несогласованной нагрузки, нигде ни теряется (за исключением потерь в фидере). Отраженная волна возвращается в источник колебаний (вычитается из падающей волны), и действие ее заключается в уменьшении мощности, потребляемой от источника колебаний. Не буду загружать читателя излишними расчетами, которые подробно описаны в [1], скажу только, что при КСВ = 3 нагрузка поглощает только 75% мощности падающей волны изза рассогласования передатчика с фидером. Необходимо подчеркнуть, что отраженная волна связана с падающей определенными соотношениями (для амплитуды и фазы), и обе они существуют в фидере одновременно (т.к. скорость их распространения очень высока). Это приводит к тому, что в фидере возникает стационарное (не меняющееся во времени) распределение тока и напряжения. На рис.2а...2и показаны эти распределения при различных значениях чисто активной нагрузки (от короткого замыкания до холостого хода), а также если эта нагрузка носит чисто индуктивный или емкостной характер.
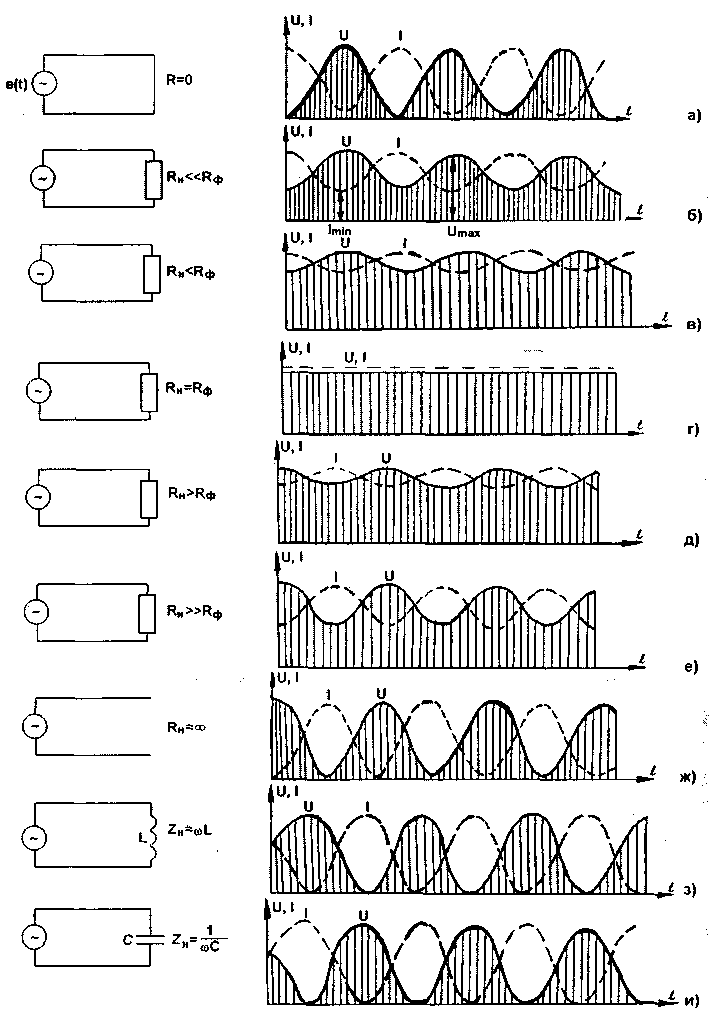
Рис. 2
При чисто реактивной нагрузке (индуктивной или емкостной) в линии устанавливается режим стоячей волны. Положение максимумов тока и напряжения зависит от индуктивного или емкостного сопротивления на конце фидера. В реальных схемах нагрузка (входное сопротивление антенны) часто бывает комплексной, те состоящей из последовательно соединенных активного и реактивного сопротивлений, но, как правило, реактивности обычно меньше активной составляющей, поэтому распределение тока и напряжения в линии приближается к распределению при активной нагрузке. При стоячих или смешанных волнах фидер по отношению к генератору имеет различное входное сопротивление. Поскольку эта картина стабильна во времени, говорят о стоячей волне. Она имеет период, равный половине длине волны (l/2). Стоячая волна характеризуется коэффициентом стоячей волны, определяемым как отношение амплитуды напряжения в максимуме к его амплитуде в минимуме, или, что абсолютно то же самое - отношение амплитуды тока в максимуме к его амплитуде в минимуме. Из этого определения первое, что приходит на ум - это измерять КСВ, измерив распределение напряжения или тока в фидере, т.е. отыскать максимальное и минимальное значение этих параметров, и, разделив одно на другое, найти значение КСВ. Если максимальное напряжение в линии (в пучности) обозначить Umax, а минимальное - Umin, КСВ может быть рассчитан по следующим формулам:
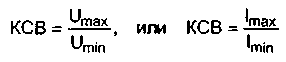
где Imax и Imin - соответственно максимальный и минимальный ток в линии. Действительно, данный метод имеет право на существование и применяется для определения КСВ в лабораторных условиях на частотах свыше 100 МГц. Для этих целей используют воздушные коаксиальные измерительные линии, оснащенные измерительными зондами. На коротких волнах этот метод в настоящее время практически не используется, поскольку длина измерительной линии должна быть по крайне мере L/2 для самой низкой рабочей частоты, что на KB составляет десятки метров. Поэтому в КВ-технике, в том числе и в любительской, применяют более простой, мостовой метод измерения КСВ (или с помощью рефлектометра). Кстати, если сопротивление нагрузки носит чисто активный характер и точно измерено, КСВ можно рассчитать, разделив сопротивление нагрузки на волновое сопротивление кабеля или сопротивление кабеля на сопротивление нагрузки (в зависимости от того, какое из двух значений больше). Этот прием широко используют на практике для калибровки КСВ-метров, нагружая их обычными безындукционными резисторами (МЛТ, ВС). Если сопротивление нагрузки больше сопротивления линии Zн >Zл, KCB = Zн/Zл. Если же Zн<Zл, то KCB = Zн/Zл.
Однако далеко не все радиолюбители вникают в физическую сущность KCB, представляющего собой отношение большего из полных сопротивлений (импедансов) к меньшему. Дело в том, что по значению KCB нельзя определить, какое из сопротивлений имеет большую величину. Например, если передатчик точно согласован с фидером 75 Ом, и при этом КСВ=3, входное сопротивление антенны, подключенной непосредственно к фидеру, может составлять и 25 Ом, и 225 Ом. При Rф = 50 Ом оно может быть в данном случае 16,7 или 150 Ом или комплексным (в зависимости от отношения длины линии к длине волны). Фактически сопротивление антенны можно измерить только специальным прибором.
(Окончание следует)
PM 11/2001