Источник: журнал QST #11, 1980

Перевод: Юрий Луцков RU3PA

Скачать статью (WinWord формат)

В предыдущих статьях о кристаллических многозвенных фильтрах экспериментальные результаты были представлены без сопутствующего теоретического анализа, так как практические трудности по измерению параметров кристалла делали эту информацию бесполезной большинству радиолюбителей. Однако сейчас существуют простые процедуры измерения, которые, вместе с множеством "конденсаторных" коэффициентов, допускают конструирование фильтров с заданной шириной полосы частот. Наборы конструктивных коэффициентов для фильтров, содержащих до восьми кристаллов, приводимые в статье сопровождаются методикой их расчета.

Частотная характеристика

На Рис. 1 показаны частотные характеристики двух разновидностей фильтров. Первая известна как максимально плоская характеристика фильтра Баттерворта, вторая с колебаниями на вершине фильтра Чебышева. В идеале число положительных пиков на втором графике должно соответствовать числу кристаллов и иметь равную амплитуду над средним значением. Однако, обычно количество пиков меньше, из-за слияния некоторых из них, а амплитуда "гребня" обычно увеличивается к скатам характеристики. Это происходит из-за разброса параметров кристаллов и конденсаторов, причем эти эффекты возрастают с увеличением порядка фильтра.

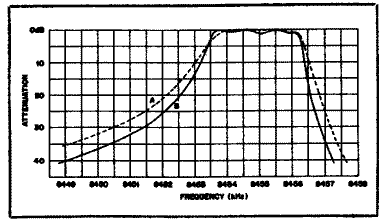
Рис.1 Частотная характеристика двух аналогичных 4-звенных фильтров. А- Баттерворта, B - Чебышева. Ширина полосы пропускания фильтра Баттерворта порядка 2369 Гц, Чебышева - 2762 Гц.

В тех случаях, когда допустима некоторая неравномерность в полосе пропускания, фильтр с характеристикой Чебышева предпочтительнее, потому что обеспечивает более высокую избирательность и имеет меньшее значение импеданса, чем фильтр Баттерворта. Этот последний фактор может быть решающим при выборе типа фильтра, который не требует применения слишком малых значений емкостей.

Коэффициентный метод конструирования фильтра

Как показано в предыдущих статьях для фильтров Баттерворта значение каждого конденсатора может быть заменено соответствующим коэффициентом, определяющим связь с "соседями", и, следовательно, частотную характеристику фильтра.
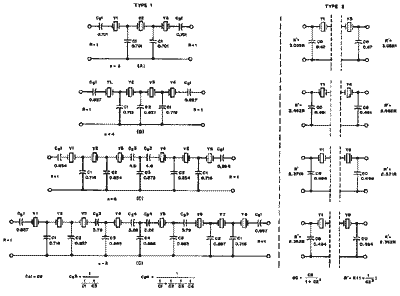
На рис. 2 приведены конструктивные коэффициенты емкостей, для фильтров Чебышева 3-го -, 4-го -, 6-го и 8го-порядков, которые были вычислены по формулам, предложенным Amstutz.

Рис.2 Коэффициенты при создании фильтров Чебышева. (щелкните мышью для получения большого изображения)

Фактические значения конденсаторов могут быть получены с использованием этих коэффициентов, по формуле

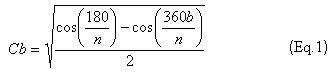
Где: k = эквивалентный коэффициент емкости,
f = центральная частота фильтра (MHz),
R = импеданс схемы (ом),
C = емкость (pF).
В высокочастотных многозвенных линиях выгоднее использовать шунтирующие конденсаторы, чем последовательные, потому что это решает проблему паразитных емкостей схемы, которые входят составной частью в шунтирующую емкость. На рис. 2 показан вариант эквивалентной замены последовательных емкостей шунтирующими, для каждого типа фильтра. К сожалению, это связано с увеличением импеданса цепи, что не всегда приемлемо.

Полоса пропускания фильтра

Одна из наиболее важных характеристик фильтра - ширина полосы частот. По методике предложенной Dishal полоса может быть определена по известному значению эквивалентной последовательной индуктивности кристалла, измерить которую достаточно сложно в любительских условиях.
Недостатком описанного ранее метода коэффициентов было то, что получение необходимой полосы пропускания достигалось экспериментально, с большими затратами времени, особенно при изготовлении фильтров высоких порядков. Однако было установлено, что можно провести начальные испытания фильтра второго порядка (с двумя кристаллами), а результаты эксперимента применить к фильтрам более высокого порядка и с другой полосой пропускания.

Начальные испытания

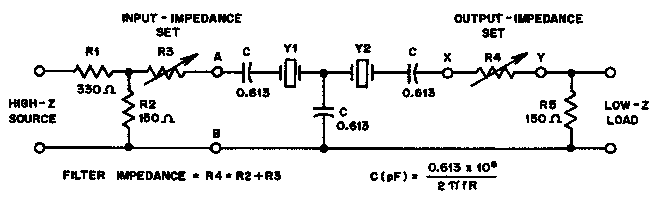
Рис. 3. Тестовая схема для определения полосы пропускания фильтра.

Схема "испытательного" фильтра приведена на рис. 3. Исходное значение емкости С, выбирают в диапазоне от 15 до 33 pF, для большинства случаев может быть принято значение 33 pF. По выбранному значению емкости определяют импеданс (комплексное сопротивление) фильтра по формуле

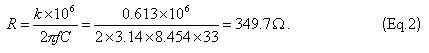
В качестве примера рассчитано сопротивление фильтра с центральной частотой 8.454 мГц и емкостью 33 pF. Это сопротивление необходимо установить с помощью резисторов R3 и R4, подключая тестер к точкам AB и XY соответственно.
Различие в схемах входной и выходной цепей объясняются особенностями использованного испытательного оборудования.

Частотная характеристика фильтра, изготовленного по предлагаемой методике, приведена на рис. 4. Провал вершины - почти теоретический около 1 dB в центре, в идеале пики с обеих сторон должны быть равны, но на практике такое случается редко из-за различий между двумя кристаллами. Однако, наиболее важный параметр, ширина полосы частот (BW1), легко измеряется на уровне -3dB (0.707 от максимума).
Следующим шагом будет уточнение значения емкости связи для фильтра с требуемой шириной полосы частот (BW2).

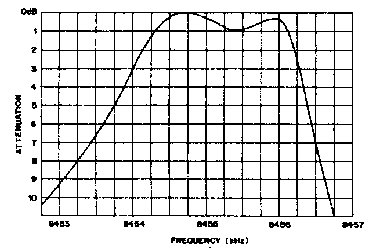
Рис.4. Типичная характеристика кварцевого фильтра с провалом на 0,9 дБ в середине фильтра и шириной полосы пропускания 2287 Гц. В идеальных условиях вершины должны быть симметричными, а провал посередине должен быть в 1 дБ.

Поскольку полученная ширина полосы частот фильтра обратно пропорциональна квадратному корню емкости связи, очень близкое приближение к точной емкости может быть вычислено по формуле

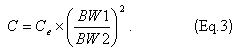
Где Ce и BW1 - емкость, и ширина полосы частот экспериментального фильтра, BW2 - требуемая полоса частот.

Затем по формуле (Eq. 2) рассчитывается новое значение импеданса по новому значению C и собирается еще один фильтр с уточненными данными. Если при последующей проверке в испытательной схеме потверждается заданное значение полосы частот, этот импеданс используется при дальнейших расчетах фильтров любого порядка по коэффициентам приведенным на рис. 2. Если не подтверждается, то необходимо еще раз пересчитать емкость по (Eq.3).

Пример расчета

Для иллюстрации предложенной методики произведем проектирование фильтра Чебышева 6-го порядка с полосой 2400 Гц. Из Таблицы 1 выберем вариант данных, полученных в результате экспериментов с фильтром 2-го порядка, с шириной полосы частот самой близкой к 2400 Гц и рассчитаем емкость C.

Таблица 1

Таблица тестовых измерений на паре кварцевых резонаторов с использованием разных величин емкостей и сопротивлений

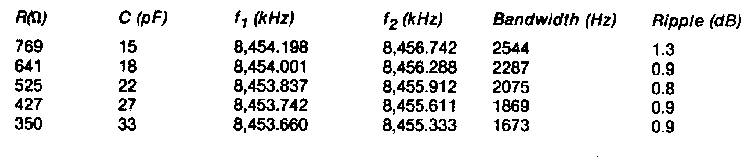
Примечание: Для каждой строчки величина сопротивления R рассчитана по формуле Eq.2

Затем определим импеданс фильтра

Используя значение импеданса рассчитаем новое значение емкостей фильтра, используя C и значения коэффициентов, приведенных на рис. 2.

подобным образом рассчитываются C2 = Cs1=22.7 pF, C3 = 23.2 pF, Cs 3=106.7 pF.
Этот фильтр был собран с использованием сверхминиатюрных кварцев с проволочными выводами и конденсаторов высокой точности. Фильтр испытывался в схеме рис. 5, полученная характеристика приведена на рис. 6. Полоса пропускания на уровне -3dB., равна 2581 Гц, что достаточно близко к желаемому результату и фильтр может быть использован в любительских целях.

Рис.5 Шестизвенный фильтр Чебышева (щелкните мышью для получения большого изображения)

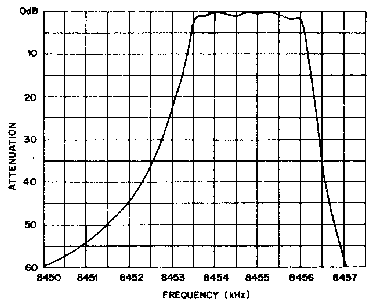
Рис. 6. Частотная характеристика шестизвенного фильтра Чебышева. Полоса пропускания по уровню -3 дБ составляет 2581 Гц, по уровню -60 дБ - 7002 Гц. Обратите внимание, что на характеристике видно только пять вершин, хотя по теории их должно быть шесть.

Компоненты

Выбор кристаллов в значительной степени ограничен. При конструировании следует учитывать, что дешевые сверхминиатюрные резонаторы требуют более высокого импеданса схемы, хотя и с такими резонаторами достижимы высокие характеристики фильтров при минимизации монтажных емкостей. В некоторых случаях положительный эффект может быть достигнут при индивидуальной подстройке емкостей.
Если есть возможность выбора, предпочтение следует отдавать резонаторам серии
HC-6/U.
Конденсаторы могут быть полистироловыми или серебряно - слюдяными. При очень малых значениях емкости, можно использовать миниатюрные подстроечные конденсаторы или отрезки кабеля.

Эволюция лестничного кварцевого фильтра

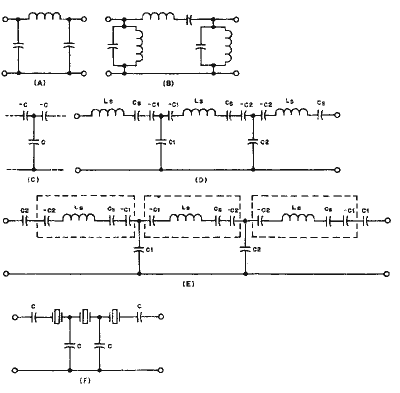
На рис. 7 представлены последовательные ступени в развитии лестничного фильтра. Прототипом является П-образный фильтр нижних частот (рис. 7A), который преобразован в полосовой фильтр (рис. 7B), добавлением катушки индуктивности к шунтирующим конденсаторам и конденсатора к последовательной индуктивности, причем все три контура настроены на одну резонансную частоту. Следующая ступень процесса использует инвертор импеданса (рис. 7C и D), который преобразует шунтирующий параллельный резонансный контур в последовательный.

Рис. 7. Эволюция трехзвенного фильтра (щелкните мышью для получения большого изображения)

Хотя инвертор импеданса использует отрицательную емкость, она поглощается большей по значению положительной емкостью, то есть, в проекте нет физически нереализуемых конденсаторов. Эта процедура была описана Cohn (7) для использования при последовательном соединении фильтров, Amstutz (4) так же использовал этот прием при проектировании узкополосных фильтров в виде ряда последовательных резонансных контуров выделенных пунктиром (рис. 7E), аппроксимированных с достаточной точностью пьезоэлектрическим кристаллом, как показано в фильтре (рис. 7F).

Вычисление коэффициентов фильтра Чебышева

Вычисления предложенные Amstutz могут иллюстрироваться следующим вычислением коэффициентов для фильтра 3-го порядка.
Зададимся допустимой амплитудой колебаний на вершине характеристики фильтра
a (dB), примем e=2.718 и n - число кристаллов.
Рассчитаем коэффициенты.

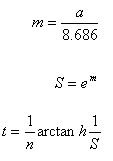
Если a=1dB и n=3, то t=0.476.
Затем определяем коэффициент импеданса фильтра по формуле

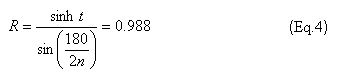
и коэффициенты конденсатора связи по формуле

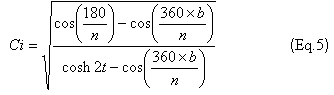
Где b=1,2,…(n-1)
Следовательно, Cl = 0.7092 и C2 = 0.7092.
Фильтр показан на рис. 8A. На следующем этапе нормализуют импеданс схемы, доводя сопротивление генератора и нагрузки до единичного и пропорционально изменяя коэффициенты конденсаторов. Результаты этого преобразования приведены на рис. 8B.
Как упомянуто ранее, последовательные конденсаторы на входе и выходе могут быть заменены шунтирующими конденсаторами как показано на рис. 8C. Они получены простым вычислением по формулам совмещенным с рисунком 8. В этом примере импеданс увеличен в 3.035 раза преобразованием схемы. Colin(1) и Pochet(3) проводили дальнейшее преобразование, нормируя импеданс с последующим перерасчетом емкостных коэффициентов. Это преобразование нами не выполнялось, чтобы сохранить простую связь между типовым и испытательным фильтрами.

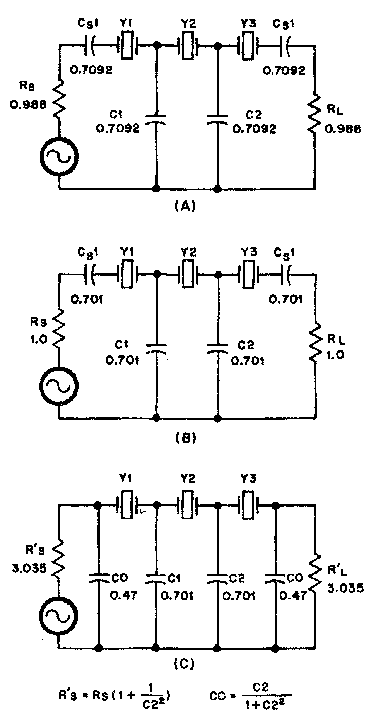
Рис. 8. Три варианта вычисления коэффициентов. На рис. 8А коэффициенты получаются из формул Eq4 и Eq5. На рис. 8B коэффициенты для фильтров первого типа нормализован для сопротивления 1 Ом. На рис. 8C представлены коэффициенты фильтров второго типа.

Фильтры Баттерворта

Нет необходимости приводить подробно этапы эволюции фильтра Баттерворта, поскольку они подобны процедуре, приведенной в предыдущем разделе. Тем не менее для тех, кто захочет проверить коэффициенты, приведенные в предыдущих статьях, приводим формулы предложенные Amstutz.

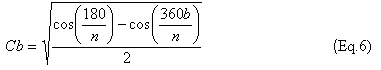
b=1,2….(n-1).

Конструктивные коэффициенты были представлены для диапазона фильтров, которые должны удовлетворять большинству любительских требований. Они были проверены при создании фильтров, использующих 2, 3, 4, 6 и 8 кристаллов, и результаты измерений подтверждают, что они ведут себя идентично фильтрам конструкции Dishal`s. Однако, необходимо отметить, что упрощенный конструктивный метод ограничен фильтрами, имеющими, относительно симметричные характеристики частоты, и однополосные фильтры должны быть разработаны, с использованием более подробной методики Dishal`s. Теперь, когда большинство экспериментальных исследований было удалено из процедуры проектирования, надеюсь, что большее количество радиолюбителей, особенно новички, получат стимул создания собственных фильтров, особенно, когда рост цен сделало коммерческие изделия почти вне досягаемости,

Квитирования

Для подтверждения приведенных рассуждений были изучены многие источники информации, перечисленные в списке использованной литературы. Это было сделано для улучшения понимания особенностей лестничных кварцевых фильтров, без чего не мог быть разработан упрощенный метод расчета ширины полосы пропускания фильтра. Автор выражает признательность А. E. Howarth за экспертную помощь при выполнения литературных поисков и переводы.

Список использованной литературы

1. Hardcastle, "Some Experiments with High-Frequency Ladder Crystal Fillers" QST, December J978 and Radio Communication (RSGBK January, February and September 1977.
2. Colin, "Formulas for the Calculation of Narrow Bandpass Fillers with Identical Piezoelectric Crystals and Maximally Flat Attenuation Behavior" (in French), Cables and Transmission, Vol. 22, April 1968,
3. Pochet, "Crystal Ladder Filters" Technical Topics, Radio Communication. September 1976 and Wireless World, July 1977.
4. Amstutz, "Narrow Band Filters" (in French), Cables and Transmission. Vol. 21, April 1967.
5. Dishal, "Modern Network Theory Design of Single Sideband Crystal Ladder Filters" Proc. IEEE, VoL 53, September 1965.
6. Hawker, "Technical Topics" Radio Communication, September 1977.
7. Cohn, "Direct Coupled Resonator Filters" Proc. IRE, February 1957.
8. Colin, "Narrow Bandpass Filters Using Identical Crystals Designed by ihe Image Parameter Method" (in French), Cables and Transmission, Vol. 21, April 1967,