Современный подход к оценке надежности изделий электронной техники
Эмануил Лидский, д. т. н., Ольга Мироненко, Андрей Гусев
В настоящее время возникло новое понимание цели расчетно-экспериментального оценивания надежности изделий электронной техники (ИЭТ). Традиционно ставилась задача прогнозирования вероятности отказа ИЭТ определенного типа. Наряду с этим появилась потребность охарактеризовать с помощью единого числового показателя надежность всей массы ИЭТ, объединяемых только единством применяемой технологии изготовления или имеющих одинаковое эксплуатационное назначение и т. п. Крупные фирмы — производители ИЭТ заинтересованы также в оценке надежности всей своей продукции в целом. Показателям надежности должна быть присвоена, помимо традиционной функции, также косвенная характеристика гарантии производителя на работу ИЭТ в течение установленного срока службы.
Особенности современного подхода рассмотрим на примере микроконтроллеров и других микросхем, изготовленных по современным технологиям [1, 2].
Чтобы обеспечить соответствие входных данных цели анализа, производится группирование продукции по принятому признаку. Так, ADI группирует весь выпуск в 9 групп, ATMEL — в 11 (по применяемой технологии). Результаты испытаний могут изучаться самостоятельно в пределах каждой группы, при объединении отдельных групп по какому-либо другому признаку или, наконец, совместно, как продукция фирмы. Столь высокая гибкость использования результатов достигается не только за счет независимости выборок, поставленных на испытания в группах, но также применением универсальных, хорошо изученных аддитивных моделей. Предполагается:
- Экспоненциальное распределение числа отказов за время испытаний.
- Представление результата испытаний в форме c2.
На языке теории групп можно сказать, что на множестве результатов испытаний выделяется с помощью оператора c2 ряд подмножеств. Элементы ряда образуют аддитивную группу. Выделение любого частичного объединения или хотя бы одного из элементов ряда дает аддитивную же подгруппу. Использование теории групп может оказаться перспективным в развитии данного подхода при обработке результатов испытаний.
Продемонстрируем построение величины c2 и особенности ее применения при оценке надежности любой подгруппы изделий. Назовем p — вероятность появления отказа, q = 1 – p. Тогда при испытании N образцов
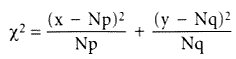 , (1)
, (1)
где x — число отказов, y = N – x.
Так как практически всегда q >> p, можно переписать (1) в виде
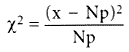 , (2)
, (2)
Известно [3], что тогда распределение числа отказов x подчинено закону Пуассона
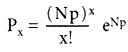 , (3)
, (3)
Из (2, 3) следует выполнение первого предположения о моделях, если выполняется второе.
Два равенства x + y = N и
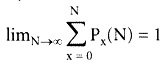
с учетом N >> 1 определяют минимальное число степеней свободы, равное 2.
При испытаниях две степени свободы отвечают 0 наблюдавшихся отказов, так как предполагалось q = 1. В этом случае распределение величины u = c2/2 будет экспоненциальным. Если в процессе испытаний был зарегистрирован отказ, то это означает, что число степеней свободы становится больше двух. Каждый отказ эквивалентен по крайней мере одному новому условию связи (речь идет о факте, считающемся непреложным). Следуя предложению ATMEL, будем считать, что каждый отказ генерирует дополнительно две степени свободы. Тогда не могут возникать дробные степени в распределении c2. Общее число степеней свободы m = 2n + 2. По мере роста числа отказов n кривая плотности c22n + 2 смещается вправо по оси u (рис. 1). Соответственно, меняются квантили распределения и возрастает вероятность отказа (в имеющихся данных приняты 60 % и 90 % уровни значимости).
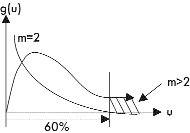
Рис. 1
С учетом изложенного вычисляется интенсивность отказов (Failure Rate)
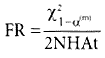 , (4)
, (4)
где N — число изделий, поставленных на испытания; H — число часов при испытании под нагрузкой; At — коэффициент ускорения. Произведение NHAt = EDH (Equivalent Device Hours).
Выражение (4) свидетельствует о высокой гибкости показателя FR.
Функции c21 – a(m) аддитивны. Нормировка с помощью EDH не влияет на аддитивность. Поэтому допустимо проводить испытания по подгруппам с последующим суммированием получаемых FR.
За основной показатель надежности принимается произведение FIT = FRx109.
(Failure in Time) число отказов за время. Множитель 109 подобран так, чтобы в расчете для всей продукции фирмы FIT был целым в пределах от 0 до 9.
Вторым основным показателем считается MTTF = 109/FIT (Mean Time to Failure) cредняя наработка до отказа.
Оба показателя, сохранив традиционные наименования, имеют вместе с тем несколько иной смысл, отвечающий требованиям, отмеченным в начале статьи.
Рассмотрим изложенное на примере, заимствованном из материалов корпорации ADI.
Из генеральной совокупности выпуска ADI взята выборка объема (Overall Sample Size) 57981
EDH = 6372926872
Число отказов (Quantity Fails) 33
m = 2n + 2 = 68
a = 60 %.
Контрольный расчет
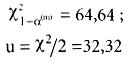
FR = 5,18x10-9 1/ч (ADI принимает для своей продукции FIT = 6).
Это определило значение множителя 109 как константы при сравнении результатов испытаний в подгруппах. Наименьшая информация была получена при испытаниях в одной из подгрупп технологии CMOS. Объем выборки — 267 образцов,
![]()
Однако рост FIT и FR не говорит о том, что данный микроконтроллер действительно менее надежен, чем другие изделия ADI. Просто ввиду недостатка информации фирма не может ручаться за тот уровень надежности, который свойственен продукции в целом.
Здесь важно отметить, что FIT может служить мерой малости выборки. Последнее часто приходится иметь в виду при планировании испытаний.
Заключение
Новые показатели надежности ИЭТ сохранили старые наименования (FR, MTTF) — интенсивность отказов, средняя наработка до отказа — но смысл их стал иным. Основой является показатель FIT, что придает всему комплексу оценок надежности сравнительный характер.
Публикуемые показатели (FIT, MTTF) могут служить традиционными оценками надежности только при условии, что они получены по результатам испытаний при большом EDH — порядка 109. В противном случае большое значение FIT свидетельствует не о физической ненадежности ИЭТ, а о малой располагаемой информации.
Показатель FIT может служить мерой малости информации, полученной при испытаниях. Интересные подтверждающие данные приведены в [4].
Литература
- www.analog.com; Corporate Information, ADI Quality Systems, MTTF and FIT Rate Calculations.
- www.atmel.com; Reliability Monitor Report, ATMEL PROPRIETARY, High Temperature Operating Life.
- Б. Л. Ван дер Варден, Математическая статистика – М: ИЛ, 1960.
- Silicon Bipolar Transistors, Reliability Data, HBFR — 405, HBFR — 420, HBFR — 450, Life Test.