Вседиапазонная КВ антенна VMA-10 NO PROBLEM

Эрнест Гуткин (UT1MA) г.Луганск

2. Приложение свойства и применение реактивной нагрузки в антенном излучателе

2.1. Термины сопротивление, волновое сопротивление.

Сопротивление коэффициент пропорциональности между напряжением и током на данном участке цепи. Например, если входное сопротивление антенны Ra=50 Ом, при любой подаваемой мощности напряжение U на входе антенны в вольтах (В) в 50 раз больше входного тока в амперах (А).

В фидерной линии коэффициент пропорциональности называется волновым сопротивлением W. К примеру, в линии с W=75 Ом в любом сечении линии отдельно для прямой и отраженной волн напряжение (В) будет в 75 раз больше тока (А).

Проводник антенны также характеризуется волновым сопротивлением W_а. Соотношение между напряжением и током в разных точках проводника разное, для расчетов применяют усредненное значение W_а. При выводе формулы для W_а используют ряд допущений, поэтому существует несколько формул, каждая из которых наиболее точна для своего вида антенн. Для вертикальных несимметричных полноразмерных антенн рекомендуется [4] формула

W_а=60[(ln2ℓ/d)-1] ,================================================================================ (П.1)

а для укороченных [5]

W_а =60ln1,15ℓ/d,================================================================================== (П.2)

где ℓ - длина и d диаметр проводника антенны.

Wa может быть определено и для отдельных частей антенны по (П.2).

Реактивная составляющая входного сопротивления вибратора зависит от длины ℓ и волнового сопротивления W_а

Х_а = W_а ctg(360+ℓ/λ)============================================================================= (П.3)

Аналогично, для верхнего участка концевой секции (КС) вибратора X_КС=W_КСctg(360+ℓ_КС/λ).

Величина активной составляющей входа антенны и вопросы согласования с фидером в данном приложении не рассматриваются.

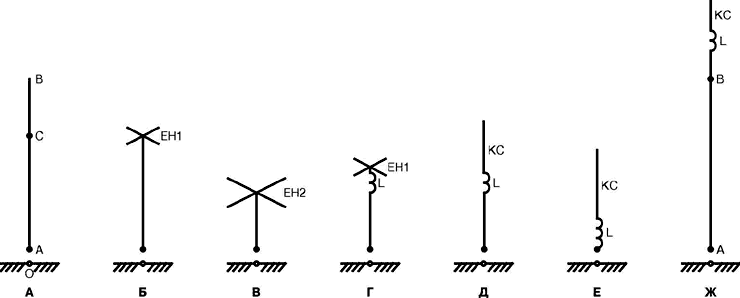
2.2. На рис.5 показаны несколько вибраторов разной конфигурации, расположенных над идеальной• землей, точки питания А О.

А. Принимаем, что первый (исходный) вибратор А-В имеет резонансную длину ℓ=λ/4.

Б. Уменьшить длину вибратора, сохранив его настройку Х_а=0, можно за счет применения т.н. емкостной нагрузки ЕН1 (рис.5б). Нагрузка характеризуется емкостным сопротивлением X_ЕН, которое зависит от количества n проводников ЕН, их длины ℓ_ЕН и диаметра d_ЕН.

В. Еще более короткий вибратор получится при использовании емкостной нагрузки больших геометрических размеров ЕН2 (рис.5в) и, соответственно, с меньшим значением │Х_ЕН│.

Г. Уменьшить величину │Х_ЕН│ нагрузки можно не только за счет увеличения размеров ЕН, но и искусственно, включив последовательно с ЕН реактивное сопротивление другого знака индуктивность L c

Х_L<│Х_ЕН│ (рис.5г). К примеру, допустим, что Х_ЕН1= -j1000 Ом и Х_ЕН2= -j400 Ом. Если добавить к ЕН1 катушку L c Х_L=j600 Ом, получим результирующую нагрузку Х_Н= -j1000+j600= -j400 Ом. Таким образом, включение индуктивности позволяет с ЕН1 меньших размеров получить эффект большей ЕН2.

Однако надо иметь в виду, что вариант Г менее широкополосный, чем предыдущие.

Пример: Считаем, что при небольшом 1% изменении частоты все реактивные нагрузочные сопротивления также изменяют свое значение на 1%. В случае понижения частоты получаем ==Х_ЕН1= -j1010, Х_ЕН2= -j404 и Х_L=j594 Ом и новое значение Х_Н= -j1010+j596= -j414 Ом. Таким образом, при чисто емкостной нагрузке изменение составило всего 4 Ома, а при комбинированной в 3,5 раза больше 14 Ом.

Д. На вибраторе= А-В (рис.5а) можно условно выделить концевую секцию (КС) В-С. Из условия равенства настроек вибраторов (рис.5а и 5б) следует, что Х_КС=Х_ЕН1. Следовательно, роль ЕН1 может выполнять и одиночный вертикальный штырь (КС), включенный выше катушки L (рис.5д). Отличие КС от ЕН состоит в том, что КС участвует в излучении, повышая тем самым эффективность вибратора. Во многих случаях применение КС более рационально, чем ЕН, т.к. на КС требуется, как правило, меньше материала и получается более простая конструкция.

Входное Х_КС по известным геометрическим размерам определяется с помощью формул (П.2) и (П.3), возможна и обратная задача по известному значению Х_КС найти её геометрические размеры, здесь возможны варианты.

Е. При равенстве (по абсолютной величине) обеих частей нагрузки Х_L=│Х_КС│ получится вибратор на рис.5е.

Ж.= Если пойти дальше и задаться нагрузочной цепью с Х_L>│Х_КС│, для сохранения= резонанса размер вибратора придется увеличить до ℓ>λ/4 (рис.5ж).

Физика процессов в рассмотренных вариантах заключается в следующем. В резонансном вибраторе длиной ℓ=λ/4 (рис.5а) поступившая из фидера очередная порция• тока при движении сохраняет фазу неизменной и только в момент отражения от конца вибратора испытывает скачок фазы на 180^О. Изменение фазы вновь поступающего из фидера тока, к моменту возвращения отраженного, также достигнет 180^О, т.е. фазы обоих токов совпадут, что и составляет суть резонанса.

При реактивной нагрузке на конце вибратора также произойдет отражение тока. Если нагрузка емкостная, фаза отраженной волны будет меньше 180^О (ток через емкость опережает напряжение), в результате для сохранения резонанса длину вибратора придется уменьшить на величину Δℓ₁ (т.е. уменьшить время движения волны по вибратору). Этот вариант иллюстрируется рис.5б,в,г. И, наоборот, если нагрузка индуктивная, фаза отраженной волны будет больше 180^О (ток через индуктивность отстает от напряжения), что потребует удлинения вибратора на величину Δℓ₂ (рис.5ж).

Для расчета Δℓ была опробована формула, применяемая в теории однородных длинных линий в случае реактивной нагрузки Х_Н на конце линии [4, 5]. По аналогии

Δℓ=(λ/360^О)arctg(W_а/Х_Н),=================================================================================== (П.4)

где Х_Н=Х_L+Х_КС (или Х_Н=Х_L+Х_ЕН), а W_а вибратора определяется его конструктивными размерами.

Проверка на макете антенны показала хорошее совпадение расчетных и опытных данных.

Пример: Применим формулу (П.4) к рассмотренным выше вариантам Б, В и Г. Расчет произведем отдельно для проволочного (Æ2мм) и трубочного (Æ40 мм) вибраторов, оба длиной 10 м. По формуле (П.1) находим

W_а-пр=60[(ln20000/2)-1)≈550 Ом, аналогично W_а-тр=313 Ом.

Для варианта Б: Х_Н=Х_ЕН1= -j1000 Ом, укорочение

Δℓ_1-ПР=(λ/360)arctg550/-1000≈0,08λ,

Δℓ_1-ТР=(λ/360)arctg313/-1000≈0,048λ.

Из этого расчета видно, что одна и та же емкостная нагрузка ЕН1 приводит к значительно большему укорочению тонкого• вибратора, чем толстого•.

Для варианта В: Х_Н=Хен2= -j400 Ом, аналогично Δℓ_1-ПР=0,15λ и Δ ℓ_1-ТР=0,1λ.

Для варианта Г: Х_Н=Х_L+Х_ЕН1= -j400 Ом, следовательно, Δℓ такие же, как в варианте В.

Отметим, что в действительности ток отражается от конца проводников ЕН, роль реактивной нагрузки заключается в соответствующем изменении фазы тока.

Вариант Ж практически не применялся по понятной причине габариты и сложность больше чем у четвертьволнового вибратора. Однако, как выяснилось, он может быть использован для 2-х частотной работы (в частности, на смежных КВ диапазонах) и в этом плане представляет несомненный интерес.

В обычной практике включенную в укороченную антенну катушку принято называть удлиняющей (при Х_L<│Х_КС│), по аналогии при Х_L>│Х_КС│ катушку можно назвать укорачивающей. Разница в поведении• определяется тем, какого вида будет результирующая реактивность связки L+КС емкостной или индуктивной. Это обстоятельство можно использовать для 2-х частотной работы, подобрав величины L и КС таким образом, чтобы на одной (низшей) частоте f_Н сопротивление связки было емкостным, а на другой (высшей) f_В индуктивным. Разместив такую связку на вершине вертикального вибратора, получим антенну, у которой вместо прежней резонансной частоты появятся два новых резонанса на частотах ниже и выше прежней.

Для антенн такого класса можно предложить название 2BLC-антенны ( 2 Band= Loading Coil антенна или

2-х диапазонная антенна с= нагрузочной катушкой ).

На рис.6 условно пунктиром показаны резонансные четвертьволновые вибраторы А-Д длиной ℓ₁ и А-В длиной ℓ₂ на частоты f_Н и f_В, а также призванный заменить их= 2BLC-вертикал в составе вибратора А-С длиной ℓ_а, катушки L и окончания КС. С учетом (П.4)

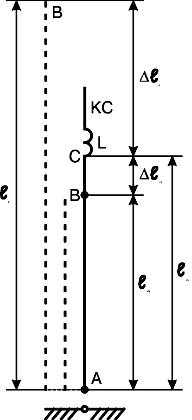
ℓ_а=ℓ₁-Δℓ₁=ℓ₁-(λ_Н/360)arctg(W_а/Х_Н1),================================================================================== (П.5)

ℓ_а=ℓ₂+Δℓ₂=ℓ₂+(λ_В/360)arctg(W_а/Х_Н2),================================================================================ (П.6)

где Х_Н1=Х_L1+Х_КС1 - суммарное реактивное сопротивление связки (нагрузки) L + КС на низшей частоте f_Н, аналогично Х_Н2=Х_L2+Х_КС2 - на высшей частоте f_В.

В результате расчета должны быть найдены величины ℓ_а, L и геометрия КС. Т.к. в двух уравнениях (П.5), (П.6) содержится 6 переменных, для расчета необходимо сделать ряд подстановок и допущений. Методика расчета выходит за рамки статьи и здесь не приводится. В частном случае, когда f_Н=0,5f_В (например, диапазоны 7 и 14 МГц) Δℓ₁+Δℓ₂=ℓ₂=0,25λ_В. В VMA-7 Δℓ₂≈0,04λ_В и Δℓ₁≈0,21λ_В=0,105λ_Н.

Распределение тока вдоль проводника 2BLC-антенны показано на рис.7. На нижней резонансной частоте f_Н (рис.7а) ток от входной точки А до катушки L изменяется незначительно, а после катушки быстро убывает.

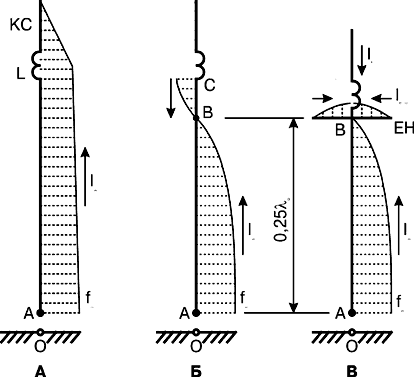
На fв (рис.7б) наличие участка (В-С) с током обратного направления во многих случаях нежелательно, так как приводит к расширению ДН. Излучение участка В-С можно исключить, применив небольшую емкостную нагрузку ЕН (рис.7в). Размеры ЕН выбирают с расчетом, чтобы Х_ЕН= -(Х_L+Х_КС ). Такую связку (ЕН+L+КС) можно рассматривать как своеобразный трап, в котором роль конденсатора выполняет ЕН, а индуктивным плечом является связка L+КС. На частоте f_Н применение ЕН практически не отражается на настройке.

Для расчета 2BLC-антенн возможно создание компьютерной программы или использование уже существующих. Впрочем, понимание внутренних взаимосвязей делает экспериментальную отработку такой двухдиапазонной антенны несложной.

При этом необходимо иметь в виду, что настройка антенны зависит не только от индуктивности катушки (измеренной на невысокой частоте, что характерно для большинства измерителей L), но и от её собственной паразитной межвитковой емкости С₀, под влиянием которой эквивалентная индуктивность цепи (катушки)= увеличивается. Например, конкретная катушка на каркасе Æ39 мм с L_В=13 мкГн (измерено прибором Е7-9) имела собственную резонансную частоту f₀=28,4 МГц (измерено ГИР#ом). Отсюда, на f₀ Х_С0= -Х_L и С₀=1/ωX_L=2,4 пФ. На частоте 14,1 МГц Х_С0= -j4690 Ом, Х_L=j1155 Ом, сопротивление цепи из параллельно включенных Х_С0 и Х_L будет Х_П=1155(-4690)/(1155 4690)=j1532 Ом и эквивалентная индуктивность L_Э14=Х_П/ω=17,3 мкГн, соответственно, на 7 МГц L_Э7=13,8 мкГн. Аналогичная катушка на каркасе Æ26 мм показала f₀=38 МГц, соответственно её эквивалентная индуктивность на частотах 7 и 14 МГц будет значительно ближе к номинальному значению 13 мкГн. Следовательно, настройка КС (т.е. её длина) будет зависеть не только от измеренной индуктивности катушки, но и от её исполнения.

Двухчастотная настройка антенны возможна и при отношении f_В к f_Н отличном от двух.

Включая последовательно несколько катушек со своими КС (или ЕН), можно получить несколько резонансных частот, как это и сделано в VMA-10.

Возможно также использование нагрузочных катушек в симметричных антеннах, в частности, в активных и пассивных элементах YAGI антенн, вместо резонансных трапов (естественно, при других размерах элементов).

2.3. Проверка правильности приведенных выше соотношений производилась на макете антенны= VMA 7 [1,= 2,= 3] с жестким противовесом ПР и радиалом Р4 (Р30/40), масштаб 1:10 ( размеры в 10 раз меньше, частоты в 10 раз выше, величины Х_КС и Х_L - без изменений). В работе использовались мостовой КСВ-метр и генератор Г4 151. Для корректности результатов были отключены проволочные вибраторы ПВ и снята емкостная нагрузка ЕН. Измеренное значение индуктивности L_В=1,3 мкГн, длина ЦВ регулировалась в широких пределах.

Были проведены следующие измерения:

1. При отключенных катушке L_В и КС изменением длины ЦВ получен резонанс на частоте f₁=70,5 МГц, при этом ℓ_ЦВ1=1250мм;

2. Аналогично, резонанс на частоте f₂=141 МГц, при этом ℓ_ЦВ2=740 мм;

3. При включенной L_В настройкой ЦВ и КС снова получены частоты резонансов 70,5 и 141 МГц, соответствующая длина ℓ_ЦВа=820 мм, длина КС из провода Æ2мм составила 205 мм.

Итого: укорочение на частоте 70,5 МГц Δℓ₁=1250 820=430 мм; удлинение на частоте 141 МГц Δℓ₂=820-740=80 мм.

Расчетная разница между ℓ_ЦВ1 и ℓ_ЦВ2 должна равняться λ2/4=2120/4=530 мм, реальная разница составляет 1250 740=510 мм. Небольшое расхождение можно объяснить разной величиной эквивалентных индуктивностей катушки Lв на частотах f₁ и f₂.

Во время измерений также фиксировалась полоса частот в пределах КСВ=2. В третьем варианте (включена L_В) полоса оказалась всего на 20+25% уже, чем в двух предыдущих. Это значительно лучше, чем при применении резонансных трапов. Использованные в эксперименте длины ЦВ1 и ЦВ2 отличались от четвертьволновых значений, что объясняется схемой VMA, но в данном случае это не имеет значения, т.к. важна была разность длин ЦВ1 и ЦВ2 по отношению к ЦВа, а не сами длины.

Параллельно проведена расчетная проверка полученных в эксперименте значений с помощью формул (П.1+П.6). Исходные данные: КС длина 205 мм при Æ2 мм, средний диаметр ЦВ 3,5 мм, частоты настройки 70,5 и 141 МГц, эквивалентные индуктивности катушки на f_Н и f_В приняты соответственно 1,35 и 1,7 мкГн.

Расчетные значения: W_КС≈305 Ом, W_ЦВ≈280 Ом. На частоте 70,5 МГц Х_КС= -j940, Х_L=j600, Х_Н= -j340 Ом и Δℓ₁=464 мм; на 141 МГц - Х_КС= -j420, Х_L=j1510, Х_Н=j1090 Ом и Δℓ₂=85.

Учитывая относительную точность формул (П.1) и (П.2) и принятых значений эквивалентных индуктивностей L_Э, совпадение расчетных данных с экспериментальными можно считать удовлетворительным.

2.4. Хотя рассмотренный выше способ создания двух- и многодиапазонных антенн вполне конкурентен• по сравнению с другими известными способами, он стал применяться только в самое последнее время, пример многодиапазонные антенны MFJ 1798 и AV 640 HY GAIN. Единственная известная автору работа на эту тему была опубликована в апрельском номере журнала QST за 1961 г. (tnx UA2BD за копию статьи). W.Lattin (W4JRW) в статье Multiband Antennas Using Loading Coils• описал 2-х диапазонную антенну на 40 и 80 м.д. в виде симметричного диполя с катушками в каждом плече. Данные из этой статьи были представлены в популярной книге [6] на стр.187. Lattin писал, что не смог обнаружить в литературе формул для определения взаимосвязи между длиной проводов, индуктивностью нагрузочных катушек и двумя резонансными частотами и свои антенны настраивал опытным путем с помощью ГИР#а. Возможно, что именно из-за неразработанности темы этот способ был предан забвению.

= Ключевые слова из заголовка пионерной статьи W4JRW =использованы автором этой статьи в предложенной выше аббревиатуре= 2BLC.

Литература.

4. Г. З. Айзенберг и др. Коротковолновые антенны•, 1985 г.

5. Х. Мейнке и Ф. Гундлах Радиотехнический справочник•, 1960 г.

6. К. Ротхаммель Антенны•, 1979 г.

7. В. Овсянников Вибраторные антенны с реактивными нагрузками•, 1985 г.

Эрнест Гуткин (UT1MA), ut1ma@mail.ru