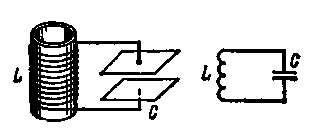
Рис.1. Простейший электрический колебательный контур.
Устройство и схема простейшего колебательного контура показаны на рис.1. Он, как видишь, состоит из катушки Ь и конденсатора С, образующих замкнутую электрическую цепь. При некоторых условиях в контуре могут возникнуть и существовать электрические колебания. Поэтому его и называют колебательным контуром.
Приходилось ли тебе наблюдать такое явление: в момент выключения питания электроосветительной лампы между размыкающимися контактами выключателя появляется искра. Если случайно соединить полосы батареи электрического карманного фонарика (чего нужно избегать), в момент их разъединения между ними также проскакивает маленькая искра. А на электростанциях, на заводах, где рубильниками разрывают электрические цепи, по которым текут очень большие токи, искры могут быть столь значительными, что приходится принимать меры, чтобы они не причинили вреда человеку, включающему ток. Почему возникают эти искры?
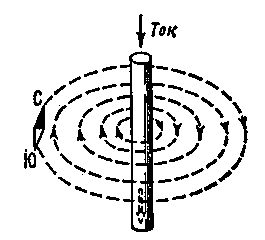
Из первой беседы ты уже знаешь, что вокруг проводника с током существует магнитное поле, которое можно изобразить в виде замкнутых магнитных силовых линий, пронизывающих окружающее его пространство (рис.2). Обнаружить это поле, если оно постоянное, можно с помощью магнитной стрелки компаса. Если отключить проводник от источника тока, то его исчезающее магнитное поле, рассеиваясь в пространстве, будет индуцировать токи в других проводниках. Ток индуцируется в в .том проводнике, который создал это магнитное поле. А так как он находится в самой гуще своих же магнитных силовых линий, в нем будет индуцироваться более сильный: ток, чем в любом другом проводнике. Направление этого тока будет таким же, каким оно было в момент разрыва проводника. Иначе говоря, исчезающее магнитное поле будет поддерживать создавший его ток до тех пор, дока оно само не исчезнет, т. е. полностью не израсходуется содержащаяся в нем энергия. Следовательно, ток в проводнике течет и после того, как выключен источник тока, но, разумеется, недолго - ничтожно малую долю секунды.
Но ведь в разомкнутой цепи движение электронов невозможно, - возразишь ты. Да, это так. Но после размыкания цепи электрическим ток может некоторое время течь через воздушный промежуток между разъединенными концами проводника, между контактами выключателя или рубильника. Вот этот ток через воздух образует электрическую искру.
Это явление называют самоиндукцией, а электрическую силу (не путай с индукцией, о которой мы говорили в первой беседе), которая под действием исчезающего магнитного поля поддерживает в нем ток,-электродвижущей силой самоиндукции или, сокращенно, э.д.с. самоиндукции.
Чем больше э.д.с. самоиндукции, тем значительнее может быть искра в месте разрыва электрической цепи.
Явление самоиндукции наблюдается не -только при выключении, но и при включении тока. В пространстве, окружающем проводник, магнитное поле возникает сразу при включении тока. Вначале оно слабее, но затем очень быстро усиливается. Усиливающееся магнитное поле тока тоже возбуждает ток самоиндукции, но этот ток направлен навстречу основному току. Ток самоиндукции мешает мгновенному увеличению основного тока и росту магнитного поля. Однако через короткий промежуток времени основной ток и проводника преодолевает встречный ток самоиндукции и достигает наибольшего значения, магнитное поле становится неизменным и действие самоиндукции прекращается.
Явление самоиндукции можно сравнивать с явлением инерции. Санки, например, трудно сдвинуть с места. Но когда они наберут скорость, запасутся кинетической энергией.- энергией движения, их невозможно остановить мгновенно. После торможения они продолжают скользить до тех пор, пока запасенная ими энергия движения не израсходуется на преодоление трения о снег.
Все ли проводники обладают одинаковой самоиндукцией? Нет! Чем длиннее проводник, тем значительнее самоиндукция. В проводнике, свернутом в катушку, явление самоиндукция сказывается сильнее, чем в прямолинейном проводнике, так как магнитное поле каждого витка катушки наводит ток не только в этом витке, но и в соседних витках этой катушки. Чем больше длина провода в катушке, тем дольше будет существовать в нем ток самоиндукции после выключения основного тока. И, наоборот, потребуется больше времена мок включения основного тока, чтобы ток в цепи возрос до определенного значения и установилось постоянное по силе магнитное поле.
Запомни: свойство проводников влиять на ток в цепи при изменении его величины называют индуктивностью, а катушки, в которых наиболее сильно проявляется это свойство, - катушками самоиндукции или индуктивности. Чем больше число витков и размеры катушки, тем больше ее индуктивность, тем значительнее влияние ее на ток в электрической; цепи. Итак, катушка препятствует как нарастанию, так и убыванию тока в электрической цепи. Если она находится в цепи постоянного тока, влияние ее сказывается только при включении и выключении тока. В цепи же переменного тока, где беспрерывно изменяются ток и его магнитное поле, э.д.с. самоиндукции катушки действует все время, пока течет ток. Это электрическое явление и используется в первом элементе колебательного контура приемника - катушке.
Вторым элементом колебательного контура приемника является "накопитель" электрических зарядов - конденсатор. Простейший конденсатор представляет собой два проводника электрического тока, это могут быть две металлические пластинки, именуемые обкладками конденсатора, разделенные непроводником электрического тока-диэлектриком, например воздухом или бумагой. Таким конденсатором ты уже пользовался во время опытов с простейшим приемником. Чем больше площадь обкладок конденсатора и чем ближе они расположены друг к другу, тем больше электрическая емкость этого прибора.
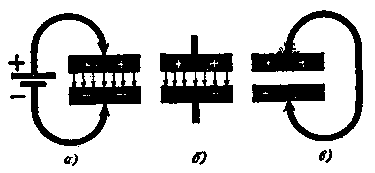
Если к обкладкам конденсатора присоединить источник постоянного тока (рис.3, а), то в образовавшейся цепи возникнет кратковременный ток и конденсатор зарядится до напряжения, равного напряжению источника тока.
Ты можешь спросить: почему в цепи, где есть диэлектрик, возникает ток? Когда мы присоединяем к конденсатору источник постоянного тока, свободные электроны в проводниках образовавшейся цепи начинают двигаться в сторону положительного полюса источника тока, образуя кратковременный поток электронов, во всей цепи. В результате обкладка конденсатора, которая соединена с положительным полюсом источника тока, обедняется свободными электронами и заряжается положительно, а другая обогащается свободными электронами, и, следовательно, заряжается отрицательно. Как только конденсатор зарядится, кратковременный ток в цепи, именуемый током заряда конденсатора, прекратится.
Если источник тока отключить от конденсатора, то конденсатор окажется заряженным (рис.3, б). Переходу избыточных электронов с одной обкладки на другую препятствует диэлектрик. Между обкладками конденсатора тока не будет, а накопленная им. электрическая энергия будет сосредоточена в электрическом доле диэлектрик а. Но стоит обкладки заряженного конденсатора соединить проводником (рис.3, в), "излишние" электроны отрицательно заряженной обкладки перейдут по этому Проводнику на другую обкладку, где их недостает, и конденсатор разрядится. В этом случае в образовавшейся цепи также возникает кратковременный ток, называемый током разряда конденсатора. Если емкость конденсатора большая, и он заряжен до значительного напряжения, момент разряда сопровождается появлением значительной искры и треска.
Свойство конденсатора накапливать электрические заряды и разряжаться через подключенные к нему проводники как раз и используется в колебательном контуре радиоприемника.
А теперь, юный Друг, вспомни обыкновенные качели. На них можно раскачиваться так, что "дух захватывает". Что для этого надо сделать? Сначала подтолкнуть, чтобы вывести качели из положения покоя, а затем прикладывать некоторую силу, но обязательно только в такт с их колебаниями. Без особого труда можно добиться сильных размахов качелей - получить большие амплитуды колебаний. Даже маленький мальчик может раскачать на качелях взрослого человека, если будет прикладывать свою силу умеючи. Раскачав качели посильнее, чтобы добиться больших амплитуд колебаний, перестанем подталкивать их. Что произойдет дальше? За счет запасенной энергии они некоторое время свободно качаются, амплитуда их колебаний постепенно убывает, как говорят, колебания затухают, и, наконец, качели останавливаются.
При свободных колебаниях качелей, так же как свободно подвешенного маятника, запасенная - потенциальная - энергия переходит в кинетическую - энергию движения, которая в крайней верхней точке вновь переходит в потенциальную, а через долю секунды - опять в кинетическую. И так до тех пор, пока не израсходуется весь запас энергии на преодоление трения веревок в местах подвеса качелей и сопротивления воздуха. При сколь угодно большом запасе энергии свободные колебания всегда являются затухающими: с каждым колебанием их амплитуда уменьшается и колебания постепенно совсем затухают -наступает покой. Но период (отрезок времени, в течение которого происходит одно колебание), а значит, и частота колебаний остаются постоянными.
Однако, если качели все время подталкивать в такт с их колебаниями В тем самым пополнять потери энергии, расходуемой на преодоление различных тормозящих .сил, колебания станут незатухающими. Это уже не свободные, а вынужденные колебания. Они будут длиться до тех пор, пока не перестанет действовать внешняя подталкивающая сила.
Я вспомнил здесь о качелях потому, что физические явления, происходящие в такой механической колебательной системе, очень схожи с явлениями в электрическом колебательном контуре. Чтобы в контуре возникли электрические колебания, ему надо сообщить энергию, которая "подтолкнула" бы электроны. Это можно сделать, зарядив, например, его конденсатор.
Разорвем выключателем В колебательный контур и подключим к обкладкам его конденсатора источник постоянного тока, как показано на рис.4 вверху. Конденсатор зарядится до напряжения батареи Б. Затем отключим батарею от конденсатора, а контур замкнем выключателем В. Явления, которые теперь будут происходить в контуре, изображены графически на рис.4 внизу.
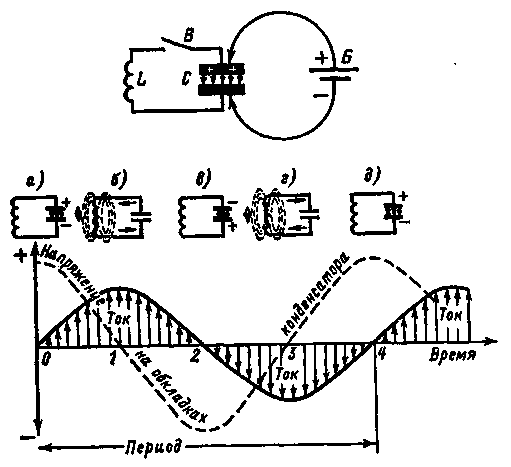
При замыкании контура выключателем верхняя обкладка конденсатора имеет положительный заряд, а нижняя - отрицательный (рис.4,а). В этот момент, отмеченный на графике точкой О, тока в контуре нет, а вся энергия, накопленная конденсатором, сосредоточена в электрическом поле между его обкладками. Но конденсатор замкнут на катушку, через которую он начнет разряжаться. В катушке появляется ток, а вокруг ее витков - магнитное поле. К моменту полного разряда конденсатора (рис.4,б), отмеченному на графике цифрой 1, когда напряжение на его обкладках упадет до нуля, ток
в катушке и энергия магнитного поля достигнут наибольших значений. Казалось бы, что в этот момент ток в контуре должен был прекратиться. Этого, однако, не произойдет, так как от действия э.д.с. самоиндукции, стремящейся поддержать ток, движение электронов в контуре будет продолжаться. Но только до тех пор, пока не израсходуется вся энергия магнитного поля. В катушке в это время будет течь убывающий по величине, но первоначального направления индуцированный ток.
К моменту времени, отмеченному на графике цифрой 2, когда энергия магнитного поля израсходуется, конденсатор вновь окажется заряженным, только теперь на его нижней обкладке - положительный заряд, а на верхней - отрицательный (рис.4,в). Теперь электроны начнут обратное движение в направлении от верхней обкладки через катушку к нижней обкладке конденсатора. К моменту 3 (рис.4,г) конденсатор разрядится, а магнитное воле катушки достигнет наибольшего значения. И опять э.д.с. самоиндукции "погонит" по проводу катушки электроны, перезаряжая тем самым конденсатор.
В момент времени 4 (рис.4,д) будет такое же состояние электронов в контуре, как в первоначальный момент 0. Закончилось одно полное колебание. Естественно, что заряженный конденсатор вновь будет разряжаться ва катушку, перезаряжаться и произойдут второе, за ним третье, четвертое в т. д. колебания. Другими словами, в контуре возникнет переменный электрический ток, электрические колебания. Но этот колебательный процесс в контуре не бесконечен. Он продолжается до тех пор, пока вся энергия, полученная конденсатором от батареи, не израсходуется ва преодоление сопротивления провода катушки контура. Такие колебания в контуре являются свободными В, следовательно, затухающими.
Какова частота этих колебаний электронов в контуре? Чтобы полнее разобраться в этом вопросе, советую провести такой опыт с простейшим маятником. Подвесь на нитке, длиной 100 см шарик, слепленный из пластилина, или ином груз массой (весом) в 20-40 г (на рис.5 длина маятника обозначена латинской буквой l). Выведи маятник из положения равновесия и, пользуясь часами с секундной стрелкой, сосчитай, сколько полных колебаний он делает за 1 мин. Примерно 30. Следовательно, частота колебаний этого маятника равна 0,5 Гц, а период - 2 с. За период потенциальная энергия маятника дважды переходит в кинетическую, а кинетическая в потенциальную. Укороти нить наполовину. Частота маятника увеличится примерно в полтора раза и во столько же раз уменьшится период колебаний.
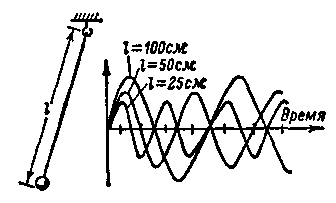
Этот опыт позволяет сделать вывод: с уменьшением длины маятника частота его собственных колебаний увеличивается, а период пропорционально уменьшается.
Изменяя длину подвески маятника, добейся, чтобы его частота колебаний была 1 Гц. Это должно быть при длине нити около 25 см. В этом случае период колебаний маятника будет равен 1 с. Каким бы ты ни пытался создать первоначальный размах маятника, частота его колебаний будет неизменной. Но стоит только укоротить или удлинить нитку, как частота колебаний сразу изменится. При одной и той же длине нитки всегда будет одна и та же частота колебаний. Это собственная частота колебаний маятника. Получить заданную частоту колебаний можно путем подбора длины нити.
Колебания нитяного маятника являются затухающими. Они могут стать незатухающими только в том случае, если маятник в такт с его колебаниями слегка подталкивать, компенсируя таким образом ту энергию, которую он затрачивает на преодоление сопротивления, оказываемого ему воздухом, энергию трения, земного притяжения.
Электрический колебательный контур тоже обладает собственной частотой. Собственная частота колебаний зависит, во-первых, от индуктивности катушки. Чем больше число витков и диаметр катушки, тем больше ее индуктивность, тем больше будет продолжительность периода каждого колебания. Собственная частота колебаний в контуре будет соответственно меньше. И, наоборот, с уменьшением индуктивности катушки сократится период колебаний - возрастет собственная частота колебаний в контуре.
Частота колебаний в контуре зависит, во-вторых, от емкости конденсатора. Чем больше емкость, тем больший заряд может накопить конденсатор, тем больше потребуется времени для его перезарядки, а это уменьшит частоту колебаний в контуре. С уменьшением емкости конденсатора частота колебаний и контуре возрастает. Таким образом, собственную частоту затухающих колебаний в контуре можно регулировать изменением индуктивности катушки или емкости конденсатора.
Но в электрическом контуре, как и в механической колебательной системе, можно получить и незатухающие, т.е. вынужденные колебания, если при каждом колебании пополнять контур дополнительными порциями электрической энергии от какого-либо источника переменного тока.
Каким же образом в контуре приемника возбуждаются и поддерживаются незатухающие электрические колебания? Током высокой частоты, возбужденным в антенне. Этот ток сообщает контуру первоначальный заряд, он же и поддерживает ритмичные колебания электронов в контуре.
Однако наиболее сильные незатухающие колебания в контуре приемника возникают- только в момент резонанса собственной частоты контура с частотой тока в антенне. Как это понимать?
Люди старшего поколения рассказывают, будто в Петербурге от шедших в ногу солдат обвалился Египетский мост. А могло это случиться, видимо, при таких обстоятельствах. Все солдаты ритмично шагали по мосту. Мост от этого стал раскачиваться - колебаться. По случайному стечению обстоятельств собственная частота колебаний моста совпала с частотой шага солдат, как говорят, мост попал в резонанс. Ритм строя сообщал мосту все новые и новые порции энергии. В результате мост настолько раскачался, что обрушился: слаженность воинского строя нанесла вред мосту. Если бы резонанса собственной частоты колебаний моста с частотой шага солдат не было, с мостом ничего бы не случилось. Поэтому, между прочим, при прохождении солдат по слабым мостам принято подавать команду "сбить ногу".
А вот опыт. Подойди к какому-нибудь струнному музыкальному инструменту и громко крикни "а": какая-то из струн отзовется-зазвучит. Та из них, которая окажется в резонансе с частотой этого звука, будет колебаться сильнее остальных струн - она-то и отзовется на звук.
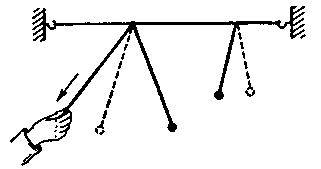
Еще один опыт - с маятниками. Натяни горизонтально нетолстую веревку. Привяжи к ней тот же маятник из нити и пластилина (рис.6). Перекинь через веревку еще один такой же маятник, но с более длинной ниткой. Длину подвески этого маятника можно изменять, подтягивая рукой свободный конец нитки. Приведи этот маятник в колебательное движение. При этом первый маятник тоже станет колебаться, но с меньшей амплитудой. Не останавливая колебаний второго маятника, постепенно уменьшай длину его подвески - амплитуда колебаний первого маятника будет увеличиваться. В этом опыте, иллюстрирующем резонанс механических колебаний, первый маятник является приемником колебаний, возбуждаемых вторым маятником. Причиной, вынуждающей первый маятник колебаться, являются периодические колебания растяжки с частотой, равной частоте колебаний второго маятника. Вынужденные колебания первого маятника будут иметь максимальную амплитуду лишь тогда, когда его собственная частота совпадает с частотой колебаний второго маятника.
Такие или подобные им явления, только, разумеется, электрического "происхождения", наблюдаются и в колебательном контуре приемника. От действия волн многих радиостанций в приемной антенне возбуждаются токи самых различных частот. Нам же из всех этих частот надо выбрать только частоту той радиостанции, передачи которой мы хотим слушать. Для этого следует так подобрать число витков катушки и емкость конденсатора колебательного контура, чтобы его собственная частота совпадала с частотой тока, создаваемого в антенне волнами интересующей нас станции. В этом случае в контуре возбудятся наиболее сильные колебания с несущей частотой той радиостанции, на волну которой он настроен. Это и есть настройка контура приемника в резонанс с частотой передающей станции. При этом сигналы других станций совсем не слышны или прослушиваются очень слабо, так как возбуждаемые ими колебания в контуре будут очень слабыми.
Таким образом, настраивая контур своего первого приемника в резонанс с частотой радиостанции, ты с его помощью как бы отбирал, выделял колебания частоты только этой станции. Чем лучше контур будет выделять нужные колебания из антенны, тем выше селективность приемника, тем слабее будут помехи со стороны других радиостанций.
До сих пор я рассказывал тебе о замкнутом колебательном контуре, т.е. контуре, собственная частота которого определяется только индуктивностью катушки и емкостью конденсатора, образующих его. Однако во входной контур любого приемника входят еще антенна и заземление. Это уже не замкнутый, а открытый колебательный контур. Дело в том, что провод антенны и Земля являются "обкладками" конденсатора (рис.7), обладающего некоторой электрической емкостью. В зависимости от длины провода и высоты антенны над землей эта емкость может быть до нескольких сотен пикофарад. Такой конденсатор на схеме рис. был показан штриховыми линиями. Но ведь антенну и землю можно еще рассматривать и как неполный виток большой катушки. Стало быть, антенна и заземление, взятые вместе, обладают еще и индуктивностью. А емкость совместно с индуктивностью образуют колебательный контур.
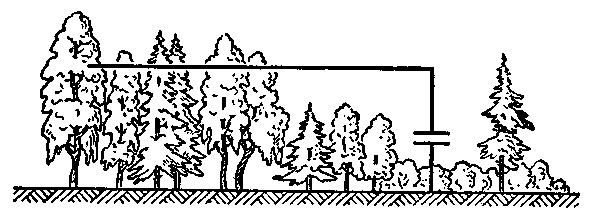
Такой контур, являющийся открытым колебательным контуром, тоже обладает собственной частотой колебаний. Включая между антенной и землей катушки индуктивности и конденсаторы, мы можем изменять его собственную частоту, настраивать его в резонанс с частотами разных радиостанций. Как это делается на практике, ты уже знаешь.
Я не ошибусь, если скажу, что колебательный контур является "сердцем" радиоприемника. И не только радиоприемника. В этом ты еще убедишься. Поэтому ему я и уделил много внимания.