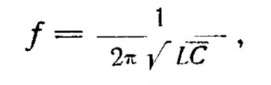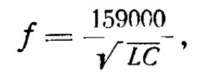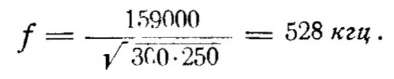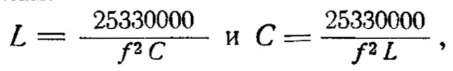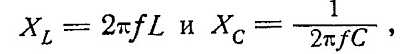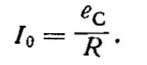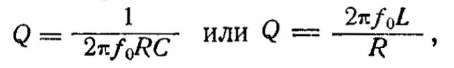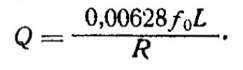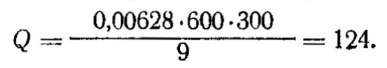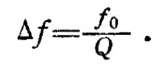Колебательный контур
Г. Шульгин
Колебательный контур, состоящий из катушки индуктивности и конденсатора, является непременной частью каждого радиоприемного и передающего устройства. Кроме того, колебательные контуры широко применяются в измерительной аппаратуре, радиотехнических приборах, предназначенных для использования в различных отраслях народного хозяйства, в электротехнических устройствах и многих других случаях.Причиной такого широкого распространения колебательного контура является одно из его замечательных свойств — способность отзываться на колебания той частоты, на которую он настроен. Ниже будут рассмотрены резонансные свойства колебательного контура, а также даны формулы для расчета некоторых из его параметров.
Собственные колебания в контуре
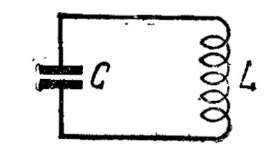
Принципиальная схема колебательного контура показана на рис. 1.
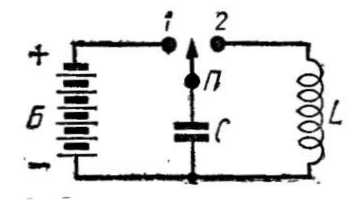
Для рассмотрения процессов, происходящих в контуре, соберем по схеме рис. 2 простой макет из батареи Б, переключателя П, катушки индуктивности L и конденсатора С. Повернув переключатель в положение 1, подключим конденсатор к батарее. Под действием напряжения UБэтой батареи конденсатор начнет заряжаться и по цепи пойдет ток. По мере заряда конденсатора напряжение UС между его обкладками будет повышаться, а ток заряда падать. Когда напряжение UС станет равным напряжению Uб конденсатор перестанет заряжаться, а ток в цепи упадет до нуля.
Рис. 1. Колебательный контурПереведем теперь переключатель в положение 2. Как только заряженный конденсатор будет подключен к катушке, он начнет разряжаться и через нее пойдет электрический ток в направлении от верхней пластины к нижней. Одновременно вокруг катушки появится магнитное поле и на ее концах образуется ЭДС самоиндукции, направленная навстречу возникшему току. Так как в начальный период скорость нарастания магнитного поля максимальна, то эта ЭДС по своему значению также оказывается максимальной и близкой к напряжению UС между обкладками конденсатора. Будучи направленной навстречу напряжению UС ЭДС самоиндукции препятствует стремительному нарастанию тока. В результате в первое мгновение ток разряда ничтожно мал и почти вся энергия, запасенная конденсатором при заряде, еще остается сосредоточенной в нем (рис. 3,а).
Рис. 2. Схема Оля пояснения процессов, происходящих в колебательном контуреДалее ток непрерывно увеличивается, энергия, запасенная в конденсаторе, убывает, переходя в энергию магнитного поля катушки, интенсивность которого продолжает нарастать (рис. 3,б). Однако скорость нарастания постепенно замедляется, вследствие чего ЭДС самоиндукции падает и все менее и менее противодействует нарастанию тока.
К моменту, когда конденсатор полностью разрядится, отдав всю накопленную энергию магнитному полю катушки, и напряжение между его обкладками станет равным нулю (рис. 3,в), ток в цепи достигнет максимального значения. Так как нарастание тока прекратится, ЭДС самоиндукции упадет до нуля.
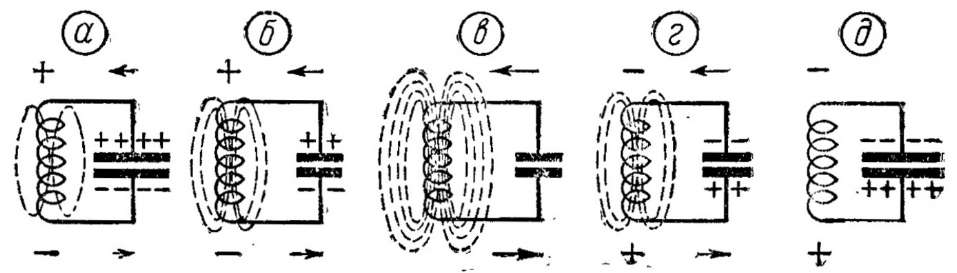
Рис. 3. Процессы, происходящие в колебательном контуре: а — энергия сосредоточена в электрическом поле конденсатора; б — в результате разряда конденсатора часть энергии перешла в магнитное поле, образовавшееся вокруг катушки; в — конденсатор полностью разрядился, вся энергия сосредоточена в магнитном поле катушки; г — конденсатор начал перезаряжаться за счет энергии магнитного поля катушки; д — конденсатор полностью перезарядилсяКазалось бы, после того как конденсатор разрядился, ток в цепи должен был бы сразу прекратиться. Однако этого не происходит. Как только ток начнет ослабевать, снова станет изменяться магнитное поле катушки, но теперь уже уменьшаясь, и на ее концах возникнет ЭДС самоиндукции, полярность которой обратна полярности предыдущей. Эта ЭДС препятствует прекращению тока. Вследствие этого в контуре в прежнем направлении продолжает протекать ток, который начинает перезаряжать конденсатор, причем нижняя пластина конденсатора приобретает положительный потенциал, а верхняя — отрицательный (рис. 3,г). Постепенно энергия магнитного поля убывает, а ток уменьшается. Когда магнитное поле катушки исчезнет, вся энергия будет возвращена в конденсатор и он окажется перезаряженным (рис. 3,д).
Теперь конденсатор опять начнет разряжаться, и весь процесс повторится; отличаться от рассмотренного он будет лишь тем, что ток через катушку пойдет в обратном направлении — от нижней обкладки к верхней и полярность напряжения на конденсаторе после перезаряда станет исходной. Таким образом в контуре произойдет полный цикл колебательного процесса. На рис. 4 графически показаны зависимости во времени между током и напряжениями в контуре.
Далее конденсатор снова начнет разряжаться и т. д. и в контуре возникнут колебания: периодически будут изменяться напряжения на конденсаторе и в катушке, ток в цепи, а энергия будет переходить из электрического поля конденсатора в магнитное поле катушки и обратно. Такие колебания в контуре принято называть собственными.
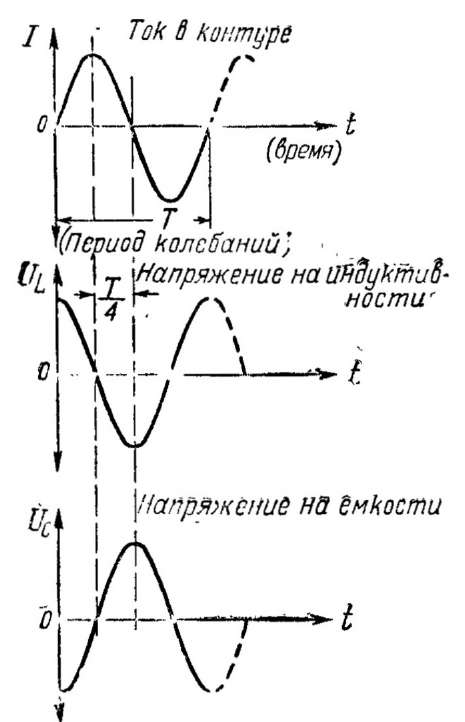
Рис. 4. Зависимости по времени между напряжениями и током в контуре:
а—ток в контуре; б — напряжение на катушке; в — напряжение на конденсатореЧастота собственных колебаний контура зависит от емкости его конденсатора и индуктивности катушки. Чем больше емкость конденсатора, тем больше времени необходимо для его разряда (заряда), а следовательно, тем меньшее число раз он успевает перезаряжаться за одну секунду и тем ниже частота собственных колебаний контура.
С другой стороны, чем больше индуктивность катушки, тем медленнее изменяется ток в контуре и тем ниже частота собственных колебаний контура.
Таким образом, с увеличением индуктивности катушки или емкости конденсатора контура частота его собственных колебаний уменьшается, а при уменьшении — возрастает. Сделав один из этих параметров переменным, можно плавно и в широких пределах менять частоту собственных колебаний контура.
Зная индуктивность и емкость контура, частоту его собственных колебаний можно подсчитать, пользуясь формулой
где f—в герцах (гц), L — в генри (гн) и С —в фарадах (ф). При расчете контуров радиоприемных и передающих устройств удобнее пользоваться формулой
в которой частота f выражена в килогерцах (кгц), L — в микрогенри (мкгн) и С —в пикофарадах (пф).
Например, если емкость контура С = 250 пф, а индуктивность L = 300 мкгн, то частота собственных колебаний окажется равной
На практике часто бывает необходимо по заданной частоте и одному из параметров контура (индуктивности или емкости) рассчитать второй. Это можно сделать по таким формулам:
где L — в мкгн, С—в пф и f—в кгц.
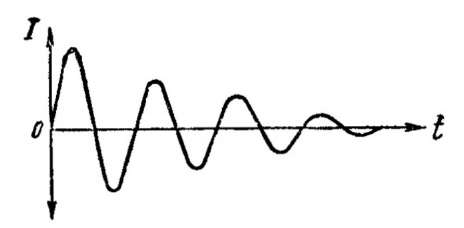
Рассматривая колебательный процесс в контуре, мы не учитывали, что часть энергии, запасенной конденсатором при заряде, расходуется на нагревание проводников и диэлектрика, на излучение и т. д. Вследствие этих потерь при каждом перезаряде конденсатор получает все меньше и меньше энергии. Если эти потери не восполнять, то при каждом последующем колебании наибольшее значение (амплитуда) тока в цепи будет уменьшаться, а через некоторое время вся энергия, полученная конденсатором от батарей при заряде, израсходуется и колебания в контуре прекратятся. Такие колебания, амплитуда которых непрерывно уменьшается, называются затухающими (рис. 5). Чем больше активное сопротивление контура и вносимые в него извне потери, тем быстрее затухают в нем колебания.
Для того чтобы получить незатухающие колебания, энергию, теряемую в контуре, тем или иным способом пополняют.
Рис. 5. Затухающие колебания в контуреИз сказанного можно сделать ряд важных выводов. Если ©вести в контур некоторую энергию, то в нем возникнут затухающие колебания. Чем больше индуктивность и емкость контура, тем ниже частота этих колебаний, и, наоборот, чем меньше индуктивность и емкость, тем частота собственных колебаний выше.
Колебания в контуре затухают тем быстрее, чем больше активное сопротивление и вносимые потери.
Напряжение на индуктивности опережает на четверть периода (рис.4), а на емкости отстает на столько же по фазе от тока в контуре. Напряжения на емкости н индуктивности по фазе противоположны,
Контур обладает избирательными свойствами
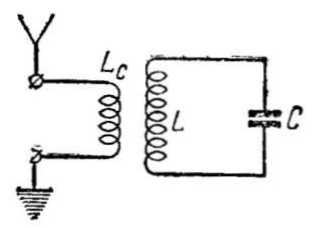
Выше мы рассмотрели случай возникновения в контуре собственных колебаний. На практике же колебательный контур часто работает в несколько иных условиях — к нему непрерывно подводится колебательная энергия извне, причем частота подводимых колебаний не всегда совпадает с частотой собственных колебаний контура. Независимо от того, каким путем энергия вводится в контур, он во всех случаях одинаково отзывается на подводимые к нему высокочастотные колебания. Рассмотрим наиболее часто применяемый в радиоприемной аппаратуре способ, при котором энергия вводится посредством специальной катушки, индуктивно связанной с катушкой контура (рис. 6). К катушке связи LС можно подключить антенну и заземление и использовать контур в качестве входной цепи приемника. Если включить катушку связи в анодную цепь лампы высокочастотного тракта, контур будет служить нагрузкой этой лампы, выделяя усиливаемые ею высокочастотные колебания.
Ток высокой частоты, проходя по катушке связи LC создает вокруг нее переменное магнитное поле, часть которого охватывает ее витки, а некоторая часть — также витки контурной катушки L. В результате в последней наводится электродвижущая сила и в цепи контура LC течет переменный ток.
Рис. 6. Введение высокочастотных колебаний в контур посредством индуктивной связиЧастота появившегося в контуре тока равна частоте подводимых колебаний и не связана с собственной частотой контура. Поэтому возникшие в контуре колебания в отличие от собственных называются вынужденными.
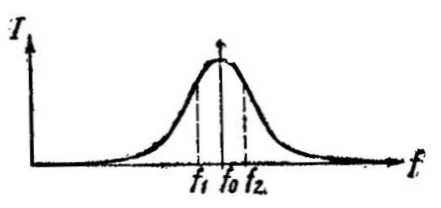
Величина тока в контуре зависит как от силы приходящих сигналов, так и от их частоты. Если изменять частоту подводимых к катушке LCколебаний, то ток в контуре будет меняться даже в том случае, когда уровень этих колебаний остается постоянным. По мере приближения частоты подводимых колебаний к собственной частоте контура ток в нем возрастает и достигает максимального значения, когда эти частоты равны (рис. 7). Дальнейшее изменение частоты приведет к уменьшению тока в контуре. Следовательно, колебательный контур является резонансным — он наиболее хорошо отзывается на колебания, частота которых равна его собственной частоте.
Частота, равная частоте собственных колебаний контура, называется резонансной частотой и обычно обозначается знаком fо.
Рис. 7. Резонансная (частотная) характеристика контураРезонансные свойства контуров широко используются в радиотехнике для разделения колебаний различных частот. В самом деле, если к катушке связи подвести несколько переменных напряжений, значительно отличающихся друг от друга по частоте, то только те колебания, частота которых близка к резонансной частоте данного контура, вызовут в нем значительный ток.
Если включить в контур конденсаор переменной емкости, то, изменяя емкость этого конденсатора, а следовательно, и частоту собственных колебаний контура, можно выделить по желанию любые из колебаний, подведенных к катушке LC. Так производится обычно настройка радиоприемника на нужную радиостанцию.
Из рис. 7, на котором показана зависимость тока в контуре от частоты подводимых колебаний, видно, что заметный ток в нем создают колебания, не только имеющие частоту fо, но и колебания других частот, сравнительно мало отличающихся от резонансной. Так, например, колебания с частотами f1 и f2 вызовут в контуре ток, всего на 30% отличающийся по величине от тока на резонансной частоте. Следовательно, колебательный контур достаточно хорошо выделяет колебания целой полосы частот. Это свойство колебательного контура очень важно для радиоприемной техники», так как передающая радиостанция излучает не одну частоту, а спектр близких друг к другу частот; все эти частоты необходимо отобрать и усилить.
Итак, колебательный контур является резонансной системой, вследствие чего он обладает избирательными свойствами. Эти свойства широко используются в технике для разделения колебаний различных частот. Способность контура выделять одновременно целую полосу близких частот делает возможным его применение в радиоприемных и радиопередающих устройствах.
Колебательный контур усиливает
При рассмотрении свободных колебаний было отмечено, что во время колебательного процесса, когда в цепи контура протекает переменный ток, на катушке и конденсаторе образуются противоположные по фазе переменные напряжения. Появление их говорит о том. что и катушка индуктивности и конденсатор представляют собой для переменного тока некоторые сопротивления, особенностью которых является то, что они не поглощают энергии. Поэтому в отличие от активного сопротивления их называют реактивными и обозначают буквой X с индексом L или С, соответственно с тем, к индуктивности или емкости данное сопротивление относится. При последовательном соединении катушки и конденсатора результирующее реактивное сопротивление Хрез цепи не увеличивается, а уменьшается и равно разности их реактивных сопротивлений
Xрез = XL — ХC
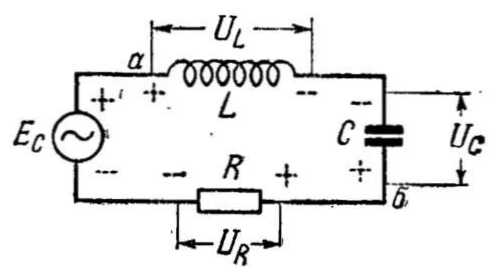
Сказанное можно пояснить эквивалентной схемой контура, приведенной на рис. 8. На схеме R — активное сопротивление контура, EС — ЭДС, введенная в контур, знаки на элементах контура показывают полярность напряжений для какого-то момента времени. Таким образом, для тока, создаваемого ЭДС контур представляет собой последовательную цепь. Так как падение напряжения на участке цепи аб, составленном из последовательно соединенных конденсатора и катушки, меньше, чем отдельно на одном из этих элементов (Uаб=UL-UС), то и реактивное сопротивление этого участка меньше реактивного сопротивления того элемента контура, напряжение на котором больше (а в частном случае и каждого из этих элементов).
Рис. 8. Эквивалентная схема колебательного контура с введенной ЭДССопротивление переменному току как катушки индуктивности, так и конденсатора зависит от частоты
где XL и ХC — сопротивления в омах, f — частота в герцах, L — индуктивность в генри и С — емкость в гарадах.
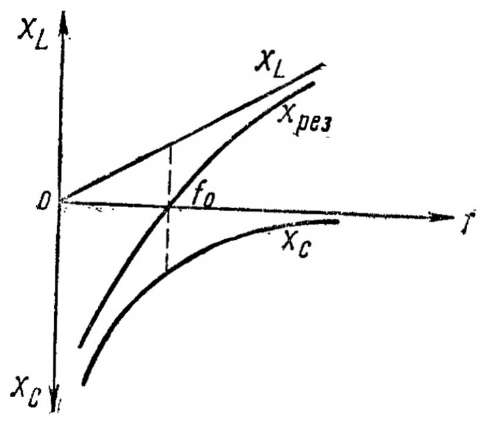
Когда частота подводимых колебаний во много раз ниже собственной частоты контура, сопротивление конденсатора переменному току велико и во много раз превышает сопротивление катушки, ток в контуре весьма мал и напряжение на катушке чрезвычайно мало, а на конденсаторе приближается к ЕC. Та же картина имеет место и при очень высокой частоте, с той лишь разницей, что в этом случае большим оказывается реактивное сопротивление катушки и напряжение на ней приближается к ЕC . При промежуточных частотах результирующее сопротивление цепи переменному току оказывается меньшим, чем на крайних частотах (рис. 9). Следовательно, большим при промежуточных частотах оказывается и ток в контуре.
Максимального значения ток в контуре достигает тогда, когда сопротивления переменному току индуктивности и емкости, а следовательно, и напряжения на них равны между собой. Происходит это потому, что в этом случае результирующее реактивное сопротивление цепи, представляющее собой разность между XL и XC, равно нулю, а полное сопротивление цепи переменному току минимально и равно только активному сопротивлению контура R
Рис. 9. Зависимость реактивных сопротивлений катушки индуктивности и конденсатора контура от частоты.
При fo XL по абсолютной величине равно XC.Такой же ток протекал бы в цепи, если бы в ней не было ни катушки, ни конденсатора, а только сопротивление R. Следовательно, все вводимое в контур напряжение выделяется на его активном сопротивлении.
Ток в контуре максимален при резонансе. Следовательно и рассмотренное явление наблюдается только при резонансе.
Реактивные сопротивления конденсатора и катушки на резонансной частоте сравнительно велики и в десятки, а иногда и сотни раз превышают активное сопротивление контура. Поэтому образующиеся на них напряжения во много раз превышают величину вводимой в контур электродвижущей силы. Сняв, например, с конденсатора контура образовавшееся на нем напряжение, мы получим большое увеличение напряжения сигнала.
Отношение напряжения на конденсаторе к электродвижущей силе еС сигнала в контуре, показывающее, во сколько раз колебательный контур усиливает напряжение сигнала при резонансе, называют добротностью контура и обозначают буквой Q. Добротность конура тем больше, чем меньше его активное сопротивление R. Ее можно вычислить по одной из формул:
где fо — резонансная частота в гц, L — индуктивность в гн, С — емкость в ф и R — активное сопротивление в ом. Если принять f0 в кгц, a L — в мкгн, то формула для Q примет вид
Например, если fо = 600 кгц, L = 300 мкгн и R = 9 ом, то добротность контура окажется равной
Добротность колебательных контуров различных конструкций, применяемых в радиоприемных устройствах, на всех диапазонах волн имеет величину одного и того же порядка и обычно лежит в пределах от 30—40 до 150—200.
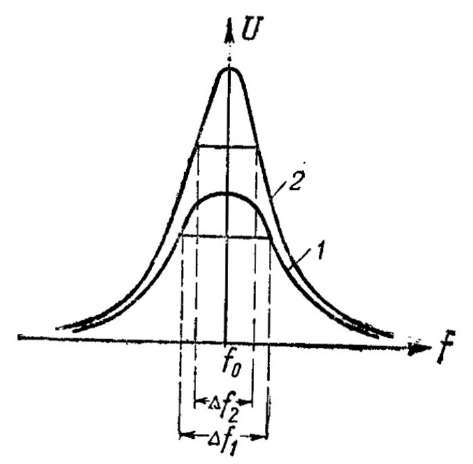
От добротности колебательного контура зависят его избирательные свойства, а также полоса частот, которую он достаточно хорошо пропускает (рис. 10). Чем выше добротность, тем острее резонансная кривая и тем лучше контур выделяет сигналы, на частоту которых он настроен. Однако при этом сужается полоса пропускаемых им частот.
За полосу пропускания Δf контура в радиотехнике обычно принимают ширину полосы частот, в пределах которой напряжение на его конденсаторе уменьшается до величины, равной 1/√2, или 0,707 от напряжения при резонансе (т. е. приблизительно на 30%). Эта полоса ровно в Q раз меньше резонансной частоты контура
Рис. 10. Зависимость формы резонансной кривой от добротности контура:
1 — резонансная кривая контура с низкой добротностью; 2 — с высокой добротностью
Полоса пропускания контура предыдущего примера равна
Δf = 600/124 =4,85 кгц или 4850 гц.
Если добротность контура очень высока, то его полоса пропускания может оказаться недостаточной для удовлетворительного приема радиопередач. Это ограничивает пределы повышения добротности контура, а следовательно и его избирательности. Невозможность одновременного получения высокой избирательности и достаточно широкой полосы пропускания является недостатком простого колебательного контура в качестве избирательного устройства приемника. Тем не менее такие контуры во многих случаях с успехом применяются.
Более совершенным избирательном устройством является система из двух и более связанных между собой колебательных контуров. Такая система позволяет полностью разрешить отмеченное выше противоречие между избирательностью и полосой пропускания.
Таким образом, чем выше добротность контура, тем больше он увеличивает напряжение сигнала и тем лучше его избирательность. Однако с повышением добротности сужается полоса пропускаемых контуром частот.
При резонансе реактивное сопротивление контура равно нулю и для источника сигнала его сопротивление оказывается активным.
[ На главную ] [ В раздел ]